并行归约问题

先解释一下什么是归约(Reduction)，归约是将某个计算问题变换为另一个问题的过程。在CUDA运算中，在向量中执行满足交换律和结合律的运算，被称为归约问题。每次迭代计算方式都是相同的（归），从一组多个数据最后得到一个数（约）^[1]^。比如当给定N个数值，求其SUM/MAX/MIN/MEAN 值的操作，也可被称为归约。

如果在CPU上，我们只需要一个循环遍历就可以实现以上操作，但使用GPU呢？

1. 将输入划分到更小的数据块中
2. 用一个Thread计算一个数据块的部分和
3. 对每个数据块的部分和，再求和，得出最终结果

上述方法通常使用迭代成对实现，具体过程见下图：

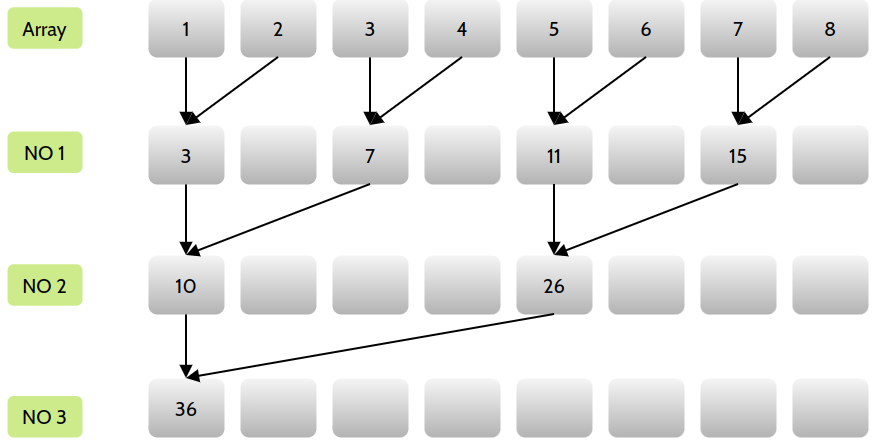
可以看出，用了三轮迭代就计算出了数组总和。

并行归约中的分化

上图是使用相邻配对方法实现的，这里有两个全局内存数组，一个大数组存放整个数组并进行归约；另一个小数组用于存放每个Block的部分和。由于归约是就地完成的，意味着在每一步全局内存中都有部分值被替换。使用 _syncthreads()可以保证Block中的任一线程在进入下次迭代之前，当前迭代中的所有部分和都被保存在全局内存中。

//这个g_idata存放的是整个数组，进行存放整个数组;g_odata 全局内存中小数组，存放每个线程块的部分和
__global__ void reduceNeighbored(int* g_idata, int* g_odata, unsigned int n) {
	//首先获取thread ID
	unsigned int tid = threadIdx.x;
	//获取idx全局编号
	unsigned int idx = blockIdx.x * blockDim.x + threadIdx.x;

	//将全局的数据指针转化为这个块的局部数据指针 idata指向某个块的开始
	int* idata = g_idata + blockIdx.x * blockDim.x;

	//数组越界检查
	if (idx >= n) {
		return;
	}

	//就地对全局数据进行规约
	for (int stride = 1; stride < blockDim.x; stride *= 2) {
		if ((tid % (2 * stride)) == 0) {
			idata[tid] += idata[tid + stride];
		}
		//它能保证线程块之间的同步问题，就是线程块中的任一线程在进入下一步迭代之前，在当前迭代里每个线程的所有部分和都被保存在全局内存
		__syncthreads();
	}
    // Block之间不能同步，因此要将Block产生的部分和返回Host
	// 将块的局部结果写到全局内存  blockIdx的范围[0,grid.x)
	if (tid == 0)
		g_odata[blockIdx.x] = idata[0];
}

其中 (tid % (2 * stride)) == 0这个判断可能不太好理解，解释一下：假设和上图一样，8个数字相加。tid编号为0-7，最开始stride=1，乘2后，只有0、2、4、6四个tid满足条件，因此这4个位置的内存，操作 idata[tid] = idata[tid] + idata[tid+stride]；随后，stride \times 2=2，只有0、2满足条件，同样执行加法操作，最后，只有0满足条件。

让我们细化到第一轮：
tid 为 0 的线程：idata[0] += idata[1]（有效，因为 0 % 2 == 0）
tid 为 1 的线程：不执行求和操作（因为 1 % 2 != 0）
tid 为 2 的线程：idata[2] += idata[3]（有效，因为 2 % 2 == 0）
tid 为 3 的线程：不执行求和操作（因为 3 % 2 != 0）
tid 为 4 的线程：idata[4] += idata[5]（有效，因为 4 % 2 == 0）
tid 为 5 的线程：不执行求和操作（因为 5 % 2 != 0）
tid 为 6 的线程：idata[6] += idata[7]（有效，因为 6 % 2 == 0）
tid 为 7 的线程：不执行求和操作（因为 7 % 2 != 0）

改善分化

由于 if ((tid % (2 * stride)) == 0) 只对偶数ID线程为 true，即只有偶数ID线程会被调度，其他线程闲置，因此会导致线程束分化。可以将访问索引修改为 int index = 2 ∗ stride ∗ tid 。注意这里仍是相邻配对，而非交错配对。

当跨度乘2后，index可以后移到有数据的内存，而非使用tid对应内存地址，减少了线程空闲。首先我们保证在一个块中前几个执行的线程束是在接近满跑的，而后半部分线程束基本是不需要执行的，当一个线程束内存在分支，而分支都不需要执行的时候，硬件会停止他们调用别人，这样就节省了资源，所以高效体现在这，如果还是所有分支不满足的也要执行，即便整个线程束都不需要执行的时候，那这种方案就无效了^[1]^。

让我们细化到第一轮：
tid 为 0 的线程：idata[0] += idata[1]（有效，因为 0 < 8）
tid 为 1 的线程：idata[2] += idata[3]（有效，因为 2 < 8）
tid 为 2 的线程：idata[4] += idata[5]（有效，因为 4 < 8）
tid 为 3 的线程：idata[6] += idata[7]（有效，因为 6 < 8）
tid 为 4 的线程：尝试 idata[8] += idata[9]（无效，因为 8 >= 8）
tid 为 5 的线程：尝试 idata[10] += idata[11]（无效，因为 10 >= 8）
tid 为 6 的线程：尝试 idata[12] += idata[13]（无效，因为 12 >= 8）
tid 为 7 的线程：尝试 idata[14] += idata[15]（无效，因为 14 >= 8）

通过对第一轮操作的细化，应该能够理解，为什么 if ((tid % (2 * stride)) == 0) 可以让Block的前半部分执行求和操作。

交错配对归约

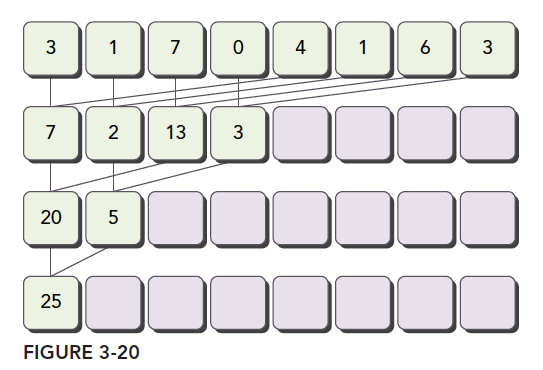
交错配对的方法，初始stride是Block大小的一半，然后每次迭代减少一半。

核心部分代码如下：

for(int stride = blockDim.x /2; stride >0; stride >>1){
	if(tid < stride){
    	idata[tid] += idata[tid] + idata[tid+stride]
    }
}

其中 stride >>1，它将 stride 的二进制表示向右移动 1 位。移出的位被丢弃，假设初始值为8，一次循环后则变为4。

展开循环

封闭的循环，可以将其迭代次数减少甚至完全消除。循环体的复制次数为循环展开因子，迭代次数变为原迭代次数/循环展开因子。

一个比较简单的例子：

for (int i = 0; i < 100; i++){
	a[i] = b[i] + c[i];
}

for (int i = 0; i < 50; i +=2){
	a[i] = b[i] + c[i];
	a[i+1] = b[i+1] + c[i+1];
}

展开的归约

在之前的归约函数中，每个Block只能处理一部分数据，但是如果能用一个Block处理更多数据，即在数据求和前，使用每个Thread进行一次加法，再从别的Block取数据，相当于先做一次向量加法，再进行归约。

__global__ void reduceUnroll2(int * g_idata,int * g_odata,unsigned int n){
	//set thread ID
	unsigned int tid = threadIdx.x;
	unsigned int idx = blockDim.x*blockIdx.x*2+threadIdx.x;
	//boundary check
	if (tid >= n) return;
	//convert global data pointer to the
	int *idata = g_idata + blockIdx.x*blockDim.x*2;
	if(idx+blockDim.x<n){
		g_idata[idx]+=g_idata[idx+blockDim.x];
	}
	__syncthreads();
	//in-place reduction in global memory
	for (int stride = blockDim.x/2; stride>0 ; stride >>=1){
		if (tid <stride){
			idata[tid] += idata[tid + stride];
		}
		//synchronize within block
		__syncthreads();
	}
	//write result for this block to global mem
	if (tid == 0)  g_odata[blockIdx.x] = idata[0];
}

g_idata[idx]+=g_idata[idx+blockDim.x]; 这行代码的作用是让每个Thread都与相邻数据块同位置的元素相加。

代码中 unsigned int idx = blockDim.x*blockIdx.x*2+threadIdx.x; 以及 int *idata = g_idata + blockIdx.x*blockDim.x*2; 在确定Block对应数据位置时有个乘2的偏移量。

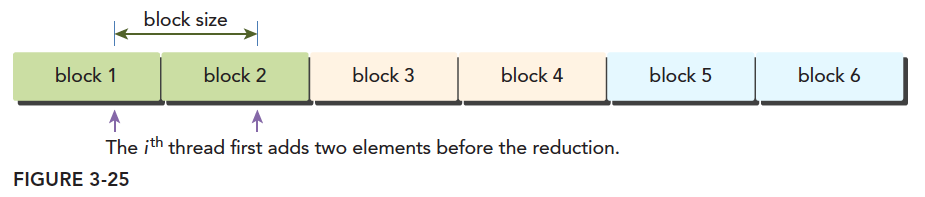
根据上图，因为只需要一半的Block来处理数据，因此全局数据索引也被调整

展开线程的归约

当只剩下32个或更少线程时，由于Warp执行是SIMT，每条指令后有隐式的Warp内同步过程。归约循环的最后6个迭代可以用下面语句：

if(tid<32){
		volatile int *vmem = idata;
		vmem[tid]+=vmem[tid+32];
		vmem[tid]+=vmem[tid+16];
		vmem[tid]+=vmem[tid+8];
		vmem[tid]+=vmem[tid+4];
		vmem[tid]+=vmem[tid+2];
		vmem[tid]+=vmem[tid+1];
	}

这个Warp展开避免了执行循环控制和线程同步。注意：一个Warp的执行进度是完全相同的，当执行 vem[tid+32] 的时候，这32个线程都在执行这步。本Warp内的所有线程都不会执行到 vem[tid+16] 。

所以要添加代码中的 volatile ，这个修饰符用来修饰变量 vmem，让编译器每次赋值时必须将 vmem[tid]的值存回全局内存中。控制变量结果写回到内存，而不是存在共享内存，或者缓存中，因为下一步的计算马上要用到它，如果写入缓存，可能造成下一步的读取会读到错误的数据。

当只剩下最后的64个数合并成1个数时，首先将前32个数，按照stride=32来进行并行加法，得到64个数字的两两之和，存在前32个数字中。

然后这32个数加上步长为16的变量，理论上，这样能得到16个数，这16个数的和就是最后这个块的归约结果^[2]^。

完全展开的归约

如果已知迭代次数，那么可以把循环完全展开。

__global__ void reduceUnrollWarp8(int * g_idata,int * g_odata,unsigned int n){
	//set thread ID
	unsigned int tid = threadIdx.x;
	unsigned int idx = blockDim.x*blockIdx.x*8+threadIdx.x;
	//boundary check
	if (tid >= n) return;
	//convert global data pointer to the
	int *idata = g_idata + blockIdx.x*blockDim.x*8;
	//unrolling 8;
	if(idx+7 * blockDim.x<n){
		int a1=g_idata[idx];
		int a2=g_idata[idx+blockDim.x];
		int a3=g_idata[idx+2*blockDim.x];
		int a4=g_idata[idx+3*blockDim.x];
		int a5=g_idata[idx+4*blockDim.x];
		int a6=g_idata[idx+5*blockDim.x];
		int a7=g_idata[idx+6*blockDim.x];
		int a8=g_idata[idx+7*blockDim.x];
		g_idata[idx]=a1+a2+a3+a4+a5+a6+a7+a8;
	}
	__syncthreads();
	//in-place reduction in global memory
	for (int stride = blockDim.x/2; stride>32; stride >>=1){
		if (tid <stride){
			idata[tid] += idata[tid + stride];
		}
		//synchronize within block
		__syncthreads();
	}
	//write result for this block to global mem
	if(tid<32){
		volatile int *vmem = idata;
		vmem[tid]+=vmem[tid+32];
		vmem[tid]+=vmem[tid+16];
		vmem[tid]+=vmem[tid+8];
		vmem[tid]+=vmem[tid+4];
		vmem[tid]+=vmem[tid+2];
		vmem[tid]+=vmem[tid+1];
	}

	if (tid == 0)  g_odata[blockIdx.x] = idata[0];
}

模板函数的归约

既然展开了最后64个数据，那也可以展开更多数据。在 __device__函数中，CUDA支持模板参数，我们可以指定展开的数量作为参数。

template <unsigned int iBlockSize>

if(iBlockSize>=1024 && tid <512)
    idata[tid]+=idata[tid+512];
__syncthreads();
if(iBlockSize>=512 && tid <256)
    idata[tid]+=idata[tid+256];
__syncthreads();
if(iBlockSize>=256 && tid <128)
    idata[tid]+=idata[tid+128];
__syncthreads();
if(iBlockSize>=128 && tid <64)
    idata[tid]+=idata[tid+64];
__syncthreads();

对于这部分代码，编译器会去检查 blockDim.x 是否固定。如果固定，则会移除不可能实现的部分。而且当 blockDim.x 确定后就不能更改了。

参考文章

[1] 【CUDA 基础】3.4 避免分支分化
[2] CUDA编程权威指针(13)-改善并行规约的分化