世界坐标系->像素坐标系
转换过程可参见这篇文章:FunnyWii's Zone 机器视觉 - 单目相机入门 ,其中描述了世界坐标系->像素坐标系的转换过程。可以归结为下述公式:
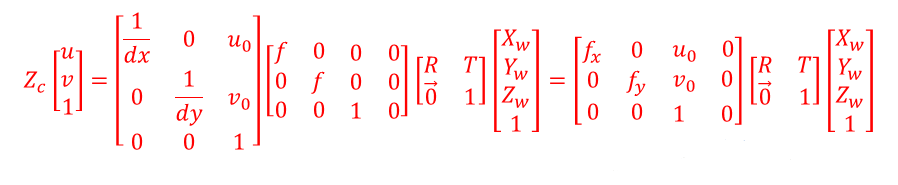
世界坐标系->像素坐标系的过程描述的是单目相机的成像原理。我们在使用单目相机的过程中,更关心的往往是像素坐标系->世界坐标系的转换过程,即还原物体的深度信息。本文基于CSDN文章像素坐标转到世界坐标时相机坐标系中的Zc值求解_相机坐标系转世界坐标系 zc怎么求-CSDN博客。在看完这篇文章之后思路打开,但是也产生了一些新疑问,这些疑问并没有在这篇文章中找到答案。我们先往下看。
像素坐标系->世界坐标系
既然有了上面的公式,那么是不是可以直接进行逆转换,就能得到世界坐标系的点了?
不是。根据公式左边, (u,v) 是已知像素坐标系的点,Z_c 是一个未知量,公式右边的 (X_w, Y_w, Z_w) 是想要知道的未知量。用2个已知量,不能求3个未知量的,换句话说,二维求三维,在这里行不通。
于是像素坐标系->世界坐标系的变换就依赖于一个很重要的假设——地面假设。即该像素点在世界坐标系中应是位于地面的,在此假设下,Z_w = 0,就变成了使用 (u,v) 求 (X_w, Y_w) ,二维转二维,可行。
简化上述公式,得到:
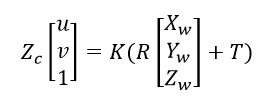
上述变换可以自行推导,我自己推导了一下,是成立的。进一步简化:
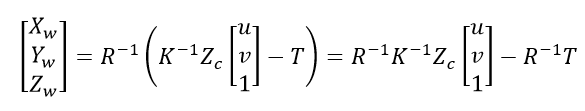
其中,K 是相机内参,R 是旋转矩阵,T 是平移向量。将这些变量用 Mat1 和 Mat2 来描述:
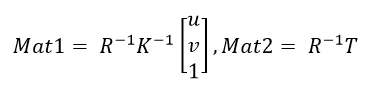
只看 Equation 2 中的 Z_w ,可以得到:
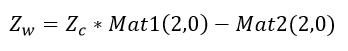
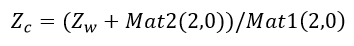
其中 Mat2 (2,0) 代表 Mat2 的第三项,注意 Mat2 是一个 3\times 1 的矩阵。如果基于地面假设,那么 Z_w 应该是 0 。
几个疑问
- 当相机坐标系和世界坐标系重合时,得到的世界坐标系为 (0, 0, 0)
理论上世界坐标系和相机坐标系当然是可以重合的,此时 T = [0, 0, 0]^T,那么 Mat2 和 Mat2 (2,0) 自然也都是 0 (Equation 3),同时由于 Z_w = 0,那么 Z_c 也就是 0 (Equation 5)。这从结果上来看并没有什么问题。
问题产生于世界坐标系和相机坐标系是可以重合的这个设定也是正确的。此时我们不要忘了:像素坐标系中的点都基于地面假设。
先假设一种极端情况,当相机坐标系和世界坐标系重合,且世界坐标系 {X-Y} 平面即相机坐标系 {X-Z} 平面都和地面重合,这种情况下既然 Z_c = 0,那么 相机坐标系->图像坐标系 的坐标变换过程中的相似三角形也就失效了,世界坐标系中的所有点坐标,根据 x \cdot Z_c = f \cdot X_c ,坐标就变成了 (0, 0, 0)。
只有 Z_w > 0 和 Z_w < 0 的点,才会有非0的世界坐标系坐标。但是基于我们的地面假设,所有像素都位于地面,整个图像中不存在 Z_w 非0的点,因此像素点的世界坐标系坐标仍然是 (0, 0, 0)。
- CSDN文章中应该能看到我的评论,关于旋转矩阵求逆后方可使用的问题。
现在公式上已经没什么问题了,如果要从源码角度实现上述转换,还需要考虑旋转的先后顺序问题。
公式中的 R 和 T 是世界坐标系->相机坐标系 的旋转矩阵和平移向量。根据旋转矩阵的定义:
其中 (\alpha , \beta, \gamma) 分别对应 R_x,R_y 和 R_z,要注意,根据坐标系正方向不同,roll, pitch, yaw 角和坐标轴的对应关系也会发生变化。而且虽然上述公式的顺序是 R_zR_yR_x,但是实际上是先进行 X 轴旋转,再 Y,最后 Z 。
先说简单的平移矩阵(向量) T ,应该是描述世界坐标系到相机坐标系原点的平移关系,一般世界坐标系以车辆后轴中心为原点。
- 结果的量纲
和平移矩阵 T 使用的量纲相同,你用 m,那么结果的单位就是 m;用 mm 结果就是 mm。
根据 Equation 5, Z_w = 0 时,量纲变为 \cfrac{Mat2 (2,0)}{Mat1 (2,0)},其中旋转矩阵 R 是没有单位的。
Mat1 中 K 中数值的单位均为 pixel,取逆后,单位变为 \cfrac{1}{pixel} ,像素坐标 (u,v) 的单位也是 pixel,相乘后抵消。因此最终结果的单位取决于 Mat2,又由于 R 没有单位,所以最终单位就取决于 T 了。
参考文章
[1] 像素坐标转到世界坐标时相机坐标系中的Zc值求解_相机坐标系转世界坐标系 zc怎么求-CSDN博客
[2] 世界坐标系、相机坐标系、图像坐标系、像素坐标系之间的转换_像素坐标与世界坐标的转换-CSDN博客

