单目相机成像原理
几个概念
- 光轴:垂直穿过理想透镜中心的光线。
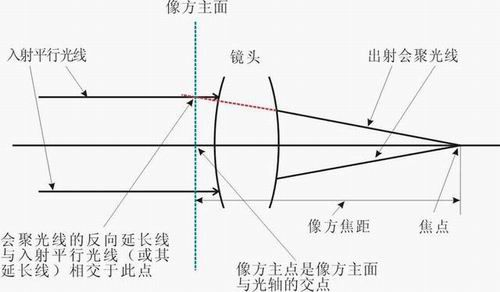
- 焦点:与光轴平行的光线射入凸透镜时,理想的凸镜应该是所有的光线会聚在透镜后面一点上,这个会聚所有光线的一点,就叫做焦点。
- 焦距:镜片的中心到焦点为止的光轴上的距离,入射平行光线(或其延长线)与出射会聚光线(或其延长线,在下图中为红色虚线)相交,就能确定折射主面,这个想象的平面与镜头光轴相交处就是主点。
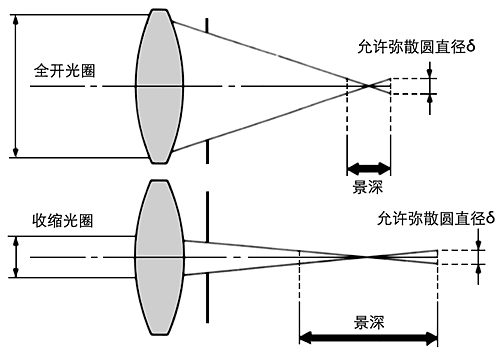
- 光圈:光圈对照片的影响主要有两大项,一是镜头的进光量,二是相片的景深。
坐标转换
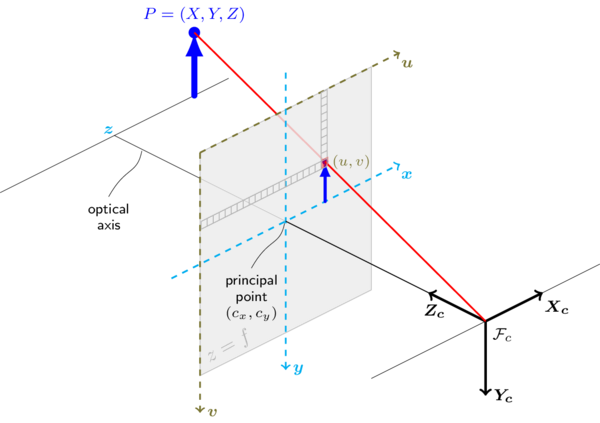
- 像素坐标系:像素坐标系以图像左上角为原点,即 u-v 坐标系。以像素为单位,使用 O_p - (u,v) 表示坐标。坐标系方向是右 u 下 v。
- 图像坐标系:图像坐标系以图像中心为原点,即 x-y 坐标系。用物理单位 O_i - (x,y) 表示像素在图像中的位置。坐标系方向是右 x 下 y。
- 相机坐标系:以相机光心为原点的坐标系,X 轴和Y 轴分别平行于图像坐标系的 X 轴和Y 轴,相机的光轴为 Z 轴。用 O_c - (x_c,y_c,z_c) 表示坐标。
- 世界坐标系:也称测量坐标系,是三维世界的绝对坐标系,描述三维环境中的任何物体的位置。O_w -(x_w,y_w,z_w) 表示其坐标。坐标系方向是“东-北-天”,即以北为车头朝向的前提下,东为 x_w,北为 y_w,上为 z_w。
图像成像是通过 世界坐标系 -> 相机坐标系 -> 图像坐标系 -> 像素坐标系 这个顺序来转换的。通常以相机光心为原点,构建坐标系:
世界坐标系 -> 相机坐标系
属于刚体变换,包括旋转和平移操作:
相机坐标系 -> 图像坐标系
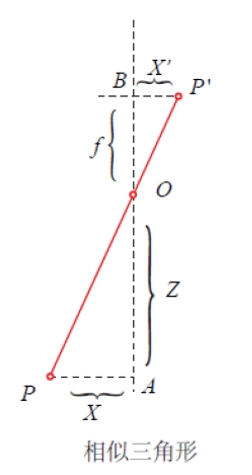
已知,相机坐标系到图像坐标系的距离为焦距 f,由相似三角形:
因此,x,y 为:
整理为齐次坐标的形式:
Z_c·\begin{bmatrix} x\\y\\1 \end{bmatrix} = \begin{bmatrix} f&0&0&0 \\ 0&f&0&0 \\ 0&0&1&0 \end{bmatrix}·\begin{bmatrix} X_c \\Y_c \\Z_c \\1 \end{bmatrix}
图像坐标系 -> 像素坐标系
图像坐标系和像素坐标系处在同一平面,但是有两点不同:
- 坐标原点不同:图像坐标系,成像平面的中心;像素坐标系,成像平面左上角
- 单位不同:图像坐标系,单位 mm,属于物理单位;像素坐标系,单位 pixel。 横向 1 pixel = dx mm,纵向 1 pixel = dy mm
图像坐标系上任意一点坐标,到像素坐标系上坐标,仅需要一次 缩放 + 平移:
其中(u,v)和(x,y)分别为像素坐标系和图像坐标系中任意一个点。
(u_0,v_0)为像素坐标系原点到图像坐标系的一个偏移量,也是内参的一部分。
即:
改写为齐次坐标形式:
\begin{bmatrix} u \\v \\1 \end{bmatrix} = \begin{bmatrix} \frac{1}{dx} &0&u_0 \\ 0& \frac{1}{dy}&v_0 \\ 0&0&1 \end{bmatrix} \begin{bmatrix} x\\y\\1 \end{bmatrix}
整合变换
整合上述变换,可得
Z_c· \begin{bmatrix} u\\v\\1 \end{bmatrix} = \begin{bmatrix} \ \cfrac{1}{dx} &0&u_0 \\ 0& \cfrac{1}{dy}&v_0 \\ 0&0&1 \end{bmatrix} \begin{bmatrix} f&0&0&0 \\ 0&f&0&0 \\ 0&0&1&0 \end{bmatrix} \begin{bmatrix} R &t \\ 0 &1 \end{bmatrix} \begin{bmatrix}X_w\\Y_w\\Z_w\\1 \end{bmatrix}
合并后,可得
Z_c· \begin{bmatrix} u\\v\\1 \end{bmatrix} = \begin{bmatrix} f_x&0&u_0 \\ 0&f_y&v_0 \\ 0&0&1 \end{bmatrix} \begin{bmatrix} R &t \\ 0 &1 \end{bmatrix} \begin{bmatrix}X_w\\Y_w\\Z_w\\1 \end{bmatrix}
其中 \cfrac{f}{dx} = f_x \, \ \cfrac{f}{dy} = f_y。这两者实际上是把焦距f的量纲转为像素数量,单位是pixle。以我目前使用120°FOV的森云相机为例,它的像素尺寸3e-3mm,焦距3mm,那么可以推断出f_x和f_y的值应该接近1000。
u_0和v_0它们表示相机光心在图像坐标系中的偏移量,以pixel为单位。
K = \begin{bmatrix} f_x&0&u_0&0 \\ 0&f_y&v_0&0 \\ 0&0&1&0 \end{bmatrix} 为相机内参矩阵K (Camera Intrinsic Matrix),描述的是物理世界与图像像素之间的变换。
T = \begin{bmatrix} R &t \\ 0 &1 \end{bmatrix} 为相机外参矩阵 (Camera Extrinsic Matrix),描述的是世界坐标系与相机之间的变换。
畸变矫正
针孔模型是一种理想的成像模型,物和像会满足相似三角关系,但是由于加工产生的误差,实际上透镜不能满足上述的三角关系,所以在图像平面上的的成像会存在一定的畸变。这种几何失真是由于焦平面上不同区域对图像的放大率不同形成的画面扭曲变形的现象,失真的程度从画面中心至画面边缘依次递增,在画面边缘最为明显。
畸变分类两种,径向畸变和切向畸变
- 径向畸变:径向畸变通常由透镜的形状造成,越向透镜边缘移动径向畸变越严重,存在桶形畸变或者枕形畸变:
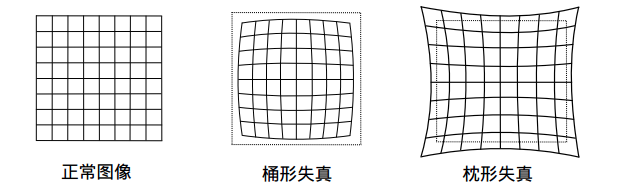
可以用r=0处的泰勒级数展开的前几项近似径向畸变。其中 k_1 k_2 k_3是径向畸变系数。径向畸变后的归一化坐标为:
- 切向畸变:切向畸变通常是在相机组装过程中透镜与成像平面不严格平行引起的,切向畸变需要两个额外的畸变参数来描述,切向畸变后的归一化坐标为:
参考文献
[1] 针孔相机模型 https://zhuanlan.zhihu.com/p/340751743
[2] 单目相机标定原理 https://blog.csdn.net/ssw_1990/article/details/53216767
[3] 相机模型:单目、双目、深度相机模型及相机畸变 https://blog.csdn.net/weixin_45929038/article/details/122882828
