Affine Transformation

仿射变换是在二维空间上对图像进行平移(Translation)、缩放(Scale)、旋转(Rotate)、错切(Shear)操作的组合。

四种变换的矩阵形式分别为：

• 平移:T_t = \begin{bmatrix} 1 & 0 & p_x \\ 0 & 1 & p_y \\ 0 & 0 & 1 \end{bmatrix}

• 旋转:T_r = \begin{bmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix}

• 缩放:T_s = \begin{bmatrix} T_x & 0 & 0 \\ 0 & T_y & 0 \\ 0 & 0 & 1 \end{bmatrix}

• 错切:T_s = \begin{bmatrix} 1 & \tan\phi & 0 \\ \tan\psi & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}

这几种变换组合之后，变换矩阵可以写成：

在这里，x、y和x'、y'分别代表变换前和变换后的点坐标。元素a_1到a_4代表旋转、缩放和错切这三种变换的组合，b_1和b_2代表平移，c_1和c_2代表透视变换，在仿射变换中是0。

可以看出，仿射变换的DOF=6，因此需要3个点对。要注意仿射变换矩阵应该是可逆的，如果不可逆，需要用一些方法去逼近这种变换。

仿射变换的特点是：相交线之间的角度可能发生变化，平行线之间的关系保持不变。

Perspective Transformation

透视变换，理解起来有些困难，文章^[5]中给出了一个很浅显易懂的例子：

手电筒朝墙上打光，手电筒正着打，墙上光斑是正圆形，斜着打是椭圆形，近了打光斑变小，远了打光斑变大。透视变换就是通过投影的方式，把当前平面上的图像映射到另外一个平面。

和Affine Transformation很明显的一个区别是，Perspective Transformation是在3维空间进行变换的，因此变换得到的图像会具备一定的(3D)空间感。此外，透视变换不保证平行线之间的平行性，但是保证点之间的共线性。

根据上述公式Eq1，透视变换DOF=8，因此需要4个点对进行变换。

下图为这两种变换的差异提供了视觉上的直观表达。

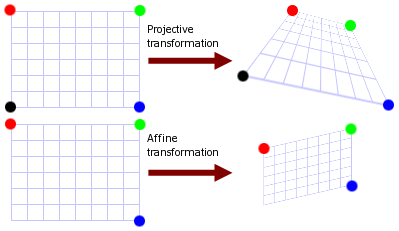
下图更详细地描述了Affine Transformation和Perspective Transformation之间的关联和差异。可以看出二者均属于Projection Transformation。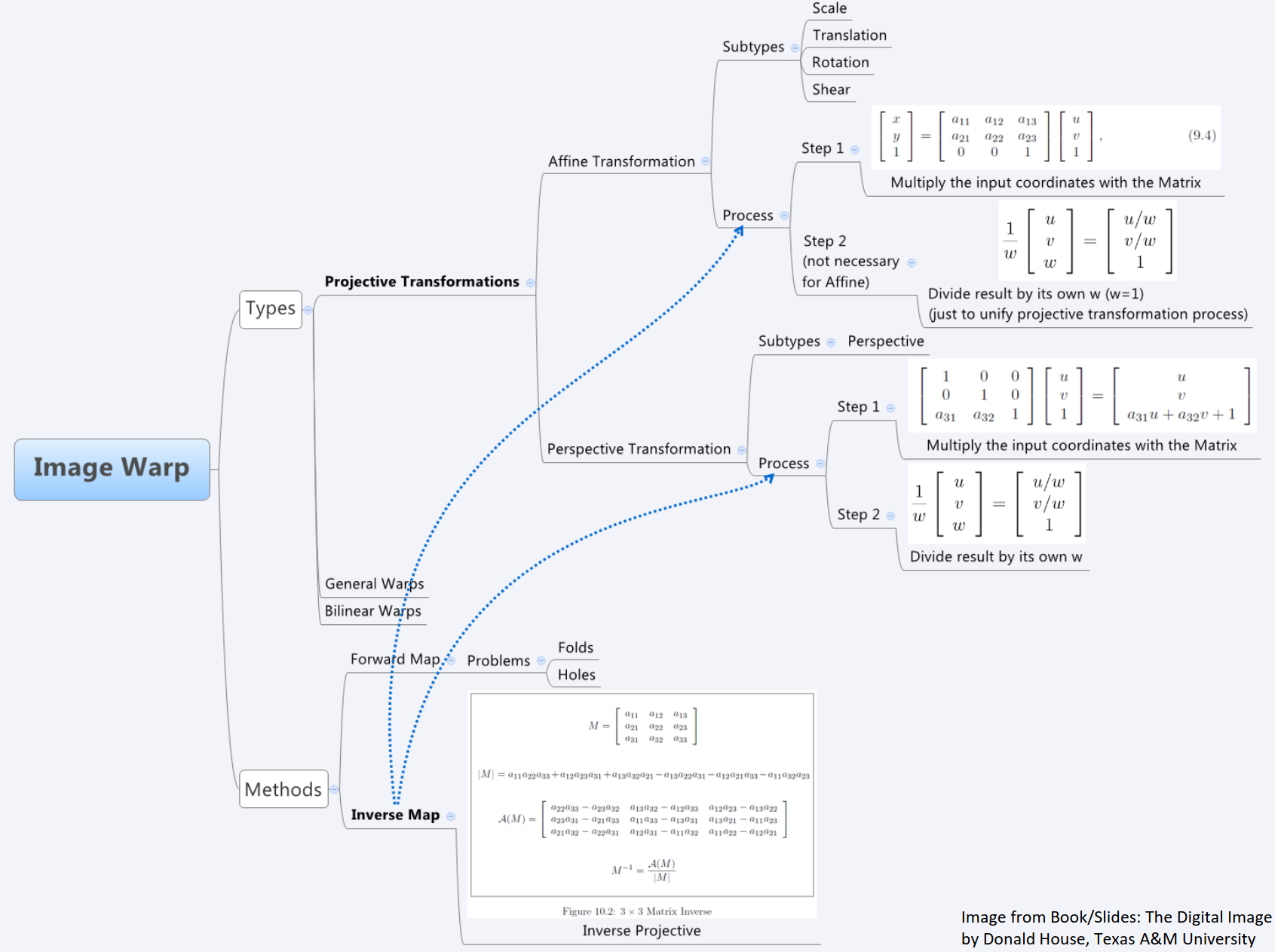

参考文章

[1] https://stackoverflow.com/questions/45637472/opencv-transformationmatrix-affine-vs-perspective-warping

[2] http://docdingle.com/teaching/cs545/presents/p12b_cs545_WarpsP2.pdf

[3] https://www.graphicsmill.com/docs/gm5/Transformations.htm

[4] https://blog.csdn.net/lx_ros/article/details/121413585

[5] https://amoko.github.io/2019/02/13/Affine-Perspective.html