方向的概念
单目相机的3D目标检测是在2D目标检测的基础上绘制出3D BBox任务,目标方向的估计是其中重要一环。
在单目相机3D视觉检测中,要理解一个重要概念:即Egocentric 自我中心和Allocentric 客体中心间的区别。这两个概念来自空间认知领域,Egocentric Frame 是基于个体自身在空间中的位置和方向。这意味着 Egocentric Frame 以个体的身体和感官输入为锚点。例如,当你站在一个房间里转头环顾四周时,你对房间中的物体的感知是基于你自己的位置和方向。你左边的物体是在你的左边,右边的物体是在你的右边,基于你自己的视角。Allocentric Frame 则基于环境中物体之间的空间关系,而不考虑个体的位置或方向。这意味着Allocentric Frame 以环境本身为锚点。例如,如果你看一张所在房间的平面图,房间中的物体会相对于彼此在地图上表示,而不是相对于你在房间内的位置或方向。
在自动驾驶领域,据 Patrick Langechuan Liu 大佬的理解,Egocentric 指相对于相机的方向,Allocentric 是相对于物体(即除自身车辆以外的目标)的方向。因此 Egocentric 也称作为车辆全局方向,因为参考系是相对于自身车辆参考系的,即使观察的对象产生变化,Egocentric 也不会变化;Allocentric 被称为局部方向或观察角,参考系会随观察对象产生变化,即对于每个物体,都有一个Egocentric Frame。
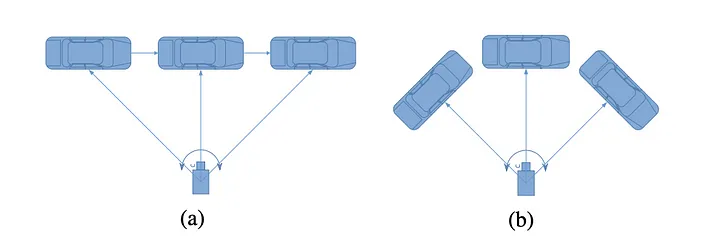
上图可以帮助理解 Egocentric 和 Allocentric。在图(a)中目标汽车全局方向都是向右的,但是当汽车移动时局部方向和形状会变化。在图(b)中目标汽车的全局方向不同,但是局部方向和形状保持不变。
可以看出单目图像中物体的外观仅取决于局部方向,而且我们只能根据外观来回归汽车的局部方向。如果要使用局部 Yaw 来计算全局 Yaw 的话,需要知道相机和目标间的光线方向,这个可以使用目标在2D图像中的位置来计算:
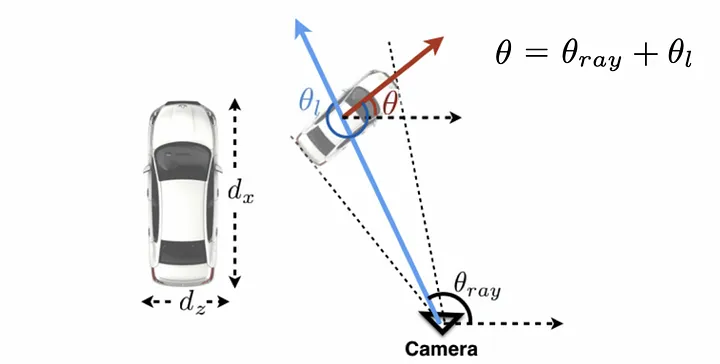
光线方向的角度可以用来自2D位置的关键点和相机的主点和焦距计算得到。2D关键点的选取规则有:
- BBox的中心,不过可能由于遮挡存在截断
- 模糊BBox的中心,对于被遮挡产生截断的物体的扩展
- 3D BBox在Pixel上的投影
- 2D BBox的底部中心(在地平面上)
若车辆离得很近或被遮挡,从而令BBox产生截断,上述方法会产生1-2度的误差。
在KITTI数据集中
检测到的物体为2D bbox提供了两个角度
\alpha: 物体的观察角度 [-\pi,\pi]
y :物体围绕 y 轴的旋转角度,在相机坐标系中的范围也是 [-\pi,\pi]
上述两个角度分别对应 allocentric 局部偏航 和 egocentric 全局偏航。
此外KITTI提供了关于方向估计的指标:Average Orientation Similarity (AOS,平均方向相似度),数值被normalize到0到1之间,数值越大,估计效果越好。具体推导过程见 cvlibs.net/publications/Geiger2012CVPR.pdf
在公式中,r = \frac{TP}{TP+FN},即recall,S(r) 被定义为:
在公式中 D(r) 为recall为 r 的所有检测物体的set,\Delta_{\theta}^{(i)} 是检测 i 的估计和ground truth间的角度差。为了避免单个物体出现多个检测bbox,若检测 i 被分配至某个重叠>50%的ground truth bbox,那么我们认为 \delta_i = 1 ,否则为0。
此外还可以用Average Angular Error(AAE,平均角度误差)来描述。见:
3D-RCNN: Instance-Level 3D Object Reconstruction via Render-and-Compare (thecvf.com)
方向的回归
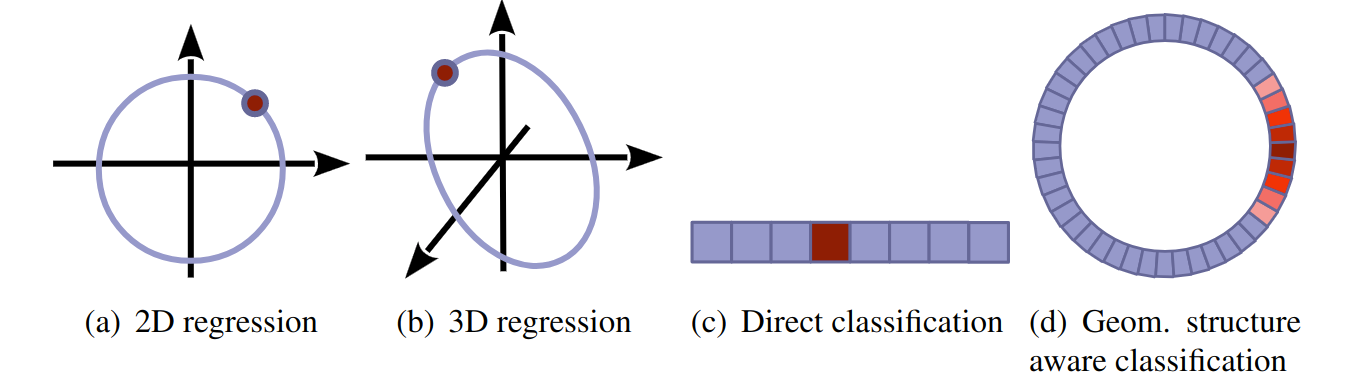
- 如使用回归方法,物体在平面上的方向可以被描述为:[\cos(\theta),\sin(\theta)]
- 至于在3D世界的方向则可以被描述为:[\cos(\theta-\frac{\pi}{3}),\cos(\theta),\cos(\theta+\frac{\pi}{3})]
- 如果使用分类的方法,那么可以直接分类到n个离散的bin里,并使用softmax cross-entropy loss。
- 或者使用几何结构感知分类,使用weighted cross-entropy loss。
3和4的主要区别是,softmax cross-entropy 只考虑一个 bin(包含ground truth)的预测,而几何感知交叉熵损失考虑所有的bin,并以 ground truth 到每个 bin 中心的距离加权。3和4都只取最高分的 bin 作为最终预测。
