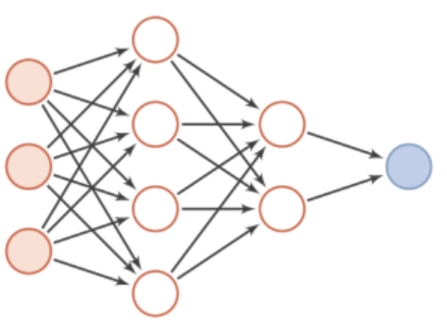
在机器学习中，如果想对对非线性函数进行建模，深度前馈网络能够实现非线性函数的建模。

在深度学习中，使用一个简单函数的深度链来学习输入数据。

线性函数的输入函数： \hat{y} = \theta^Tx

非线性函数的输入函数：\hat{y} = f(\phi(x);\theta)

其中，\phi(x) = h^{(m)}(...(h^{(2)}(h^{(1)}(x))))

\phi 是输入数据 x 的学习表征，h(x) 是激活函数。

深度前馈网络

在深度前馈网络的每一层（Layer），使用一个简单的线性函数 W^{l} x^{(l-1)} 和后面的激活函数 h(x)来表示网络结构。

网络的整体结构：

在每层中：

每一层都会使用一个简单的线性函数及一个权重矩阵W

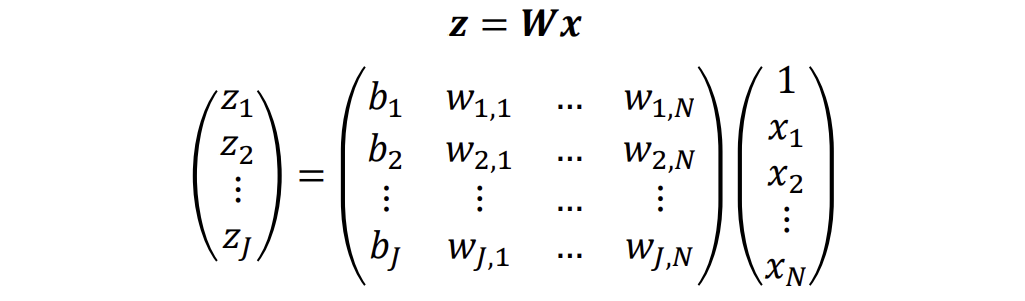
隐藏单元的激活函数 Activation Functions

h(.) 是激活函数

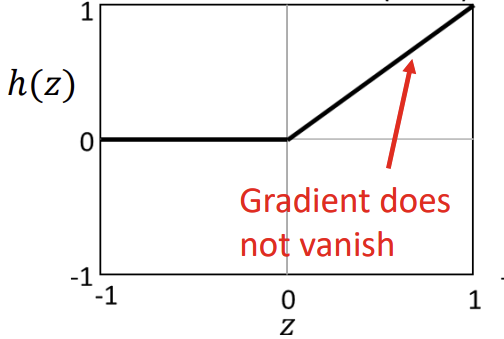
ReLU

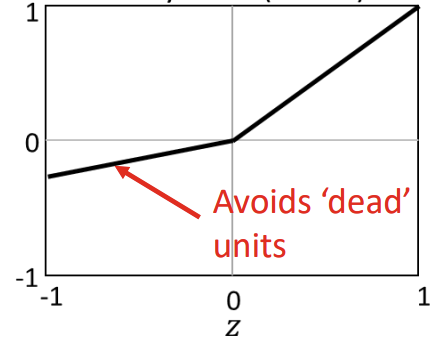
LReLU

Sigmoid

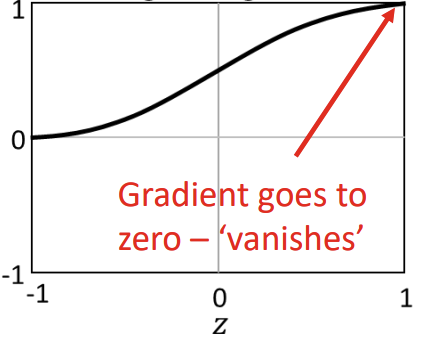
Tangent

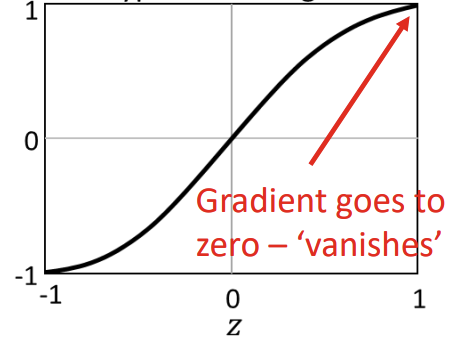
输出单元

回归问题，是线性输出

分类（class>2）问题，是SOFTMAX输出，softmax的输出用来预测各个分类的可能性

深度前馈网络是一个具有非线性激活函数的线性函数链，有一个专门用于任务的输出层，即回归或分类。

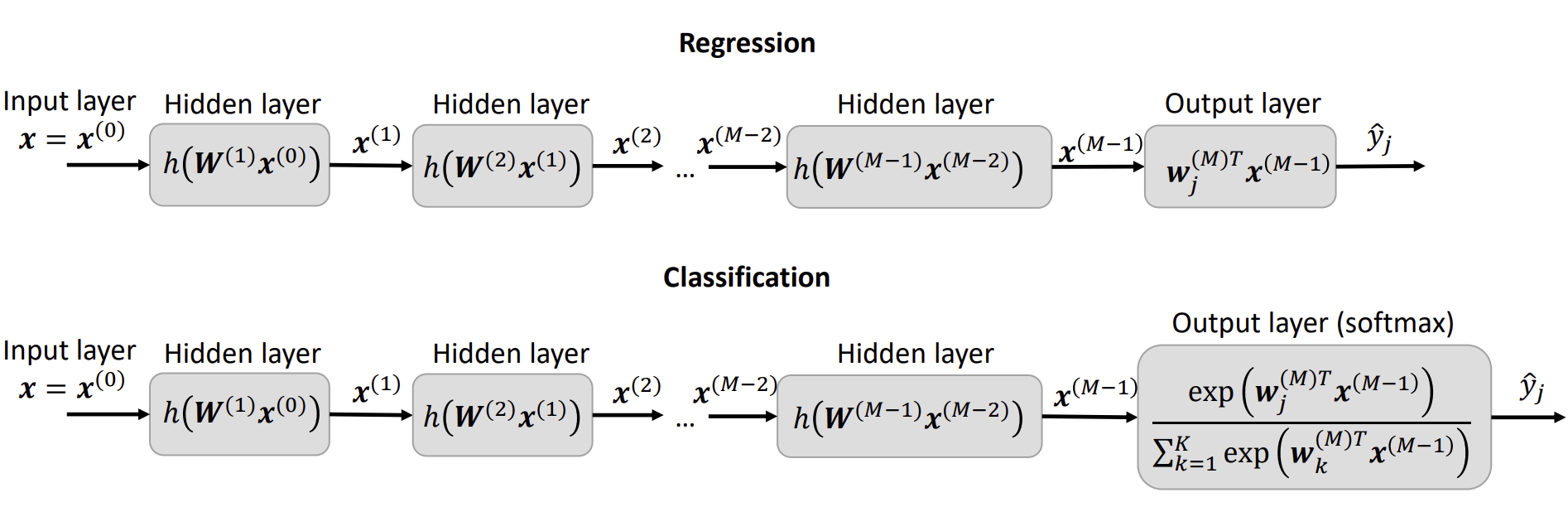
反向传播 Back Propagation

反向传播又被称为BP，允许来自cost function的信息通过网络向后流动，以便计算梯度（Gradient）。

SGD

用下面的公式不断更新w的值：

这里的L_n是一个sample的Loss

对于深度前馈网络，\delta_j^{(l)}x_i^{(l-1)} 可以被替换为 \frac{\partial L_n}{\partial w_{ji}^{(l)}}

推导过程如下：

首先回想起在每个单元，前馈输出 z^{(l)} = W^{(l)}x^{(l-1)}

根据链式法则，

由上面两个公式可以得到 \frac{\partial L_n}{\partial w_{ji}^{(l)}} = \delta_j^{(l)} x_i^{(l-1)}

根据上面的公式，SGD可以更新：

现在只要求出\delta_j^{(l)} 就可以得到BP的完整表达式。

因此，

由于

因此

w_{kj}^{(l)} h'(z_j^{(l-1)})可以替换原本公式中的 \frac{\partial z_k^{(l)}}{\partial z_j^{(l-1)}}:

因此

反向传播算法

1. 正向传播，估计 \forall l

   z_k^{(l)} = w_j^{(l)T}x_i^{(l-1)}
   x_j^{(l)} = h(z_j^{(l)})

2. 初始化\delta^{(M)}

   \delta^{(M)} = \frac{\partial L_n}{\partial y_j}f'(z_j^{(M)})

   也就是 \hat{y}-y

3. 反向传播

   每层都计算一次

4. 梯度

   frac{\partial L_n}{\partial w_{ji}^{(l)}} = \delta_j^{(l)}x_i^{(l-1)}

   假设 \frac{\partial L_n}{\partial w_{ji}^{(l)}} 为 G 的话，接下来在每层， w会更新：

   w^{(l)} = w^{(l)} - \epsilon G

maxIter = m;
for epoch = 1:maxEpochs % loop over number of epochs
    loss = [];
    for iter = 1:m % loop over all data samples
        %% 1. forward propagation
        net(1).x = x(r(iter)); % extract random input
        for l = 2:M % loop over each layer
            net(l).z = net(l).W*[1; net(l-1).x]; % weight & bias
            net(l).x = max(net(l).z,0); % ReLU activation
        end
        net(M).yhat = net(M).z; % output activation
        %% 2. initialise delta
        net(M).delta = (net(M).yhat-y(r(iter)));
        %% 3. backpropagation through all network layers
        for l = M:-1:3
            net(l-1).delta = net(l).W(:,2:end)'*net(l).delta.*(1.*(net(l-1).z>0));
        end
        %% 4. define loss function gradient
        for l = 2:1:M
            net(l).grad = [net(l).delta net(l).delta*net(l-1).x']; % additional layers
        end
        %% update parameters using SGD
        for l = 2:M
            G = net(l).grad; % error gradient matrix
            net(l).W = net(l).W - epsilon.*G; % SGD update rule
        end
        %% plot results: evaluate and plot loss
        for i = 1:m % forward propagate all data
            net(1).x = x(i); % extract data input sample
            for l = 2:M % loop over network layers
                net(l).z=net(l).W*[1;net(l-1).x]; % weight and bias
                net(l).x=max(net(l).z,0); % ReLU activation
            end
            net(M).yhat=net(M).z; % output
            Yhat(i) = net(M).yhat; % store output
        end
        loss(iter) = sum((Yhat - y).^2); % evaluate loss
        figure(101);subplot(1,2,1); cla; plot(loss); xlabel('Iteration'); ylabel('Loss');
        title(['(a) Loss (Epoch: ' num2str(epoch) ')']); xlim([0 maxIter]);
        subplot(1,2,2); cla; plot(x,y,'.'); hold on; plot(x,Yhat);
        xlabel('x'); ylabel('y'); title('(b) Model Fit'); drawnow;
    end
end