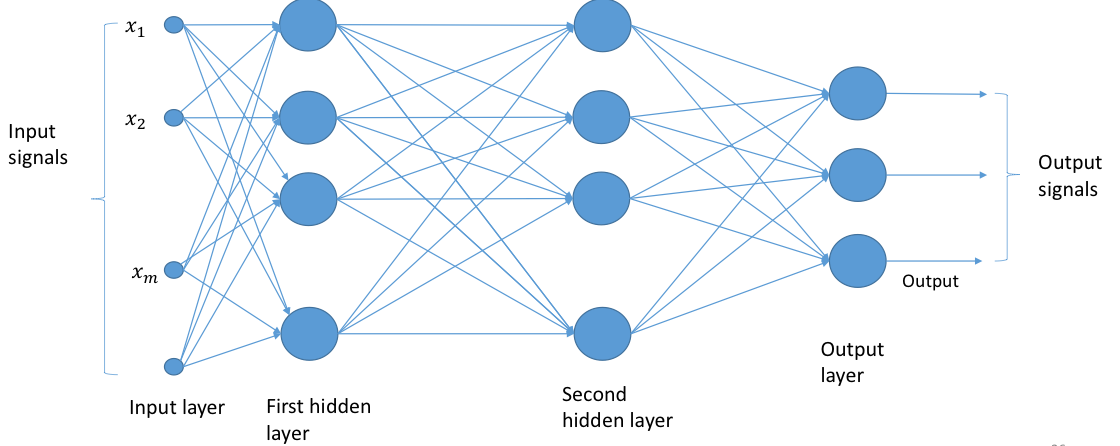
Neural Networks, NN

1943年 Warren McCulloch 和 Walter Pitts 设计了人工神经网络（artificial neural network，ANN），通常简称为神经网络（NN）。ANN是受构成动物大脑的生物神经网络模糊启发的计算系统，但是每个神经元上的参数还需要人为指定。

Frank Rosenblatt 后来提出了感知机（Perception），和NN类似，输入经过神经元被乘权重并求和，但是在NN的基础上，加入了偏置项（bias），求和结果会加上bias，最后经过激活函数得到最终输出。

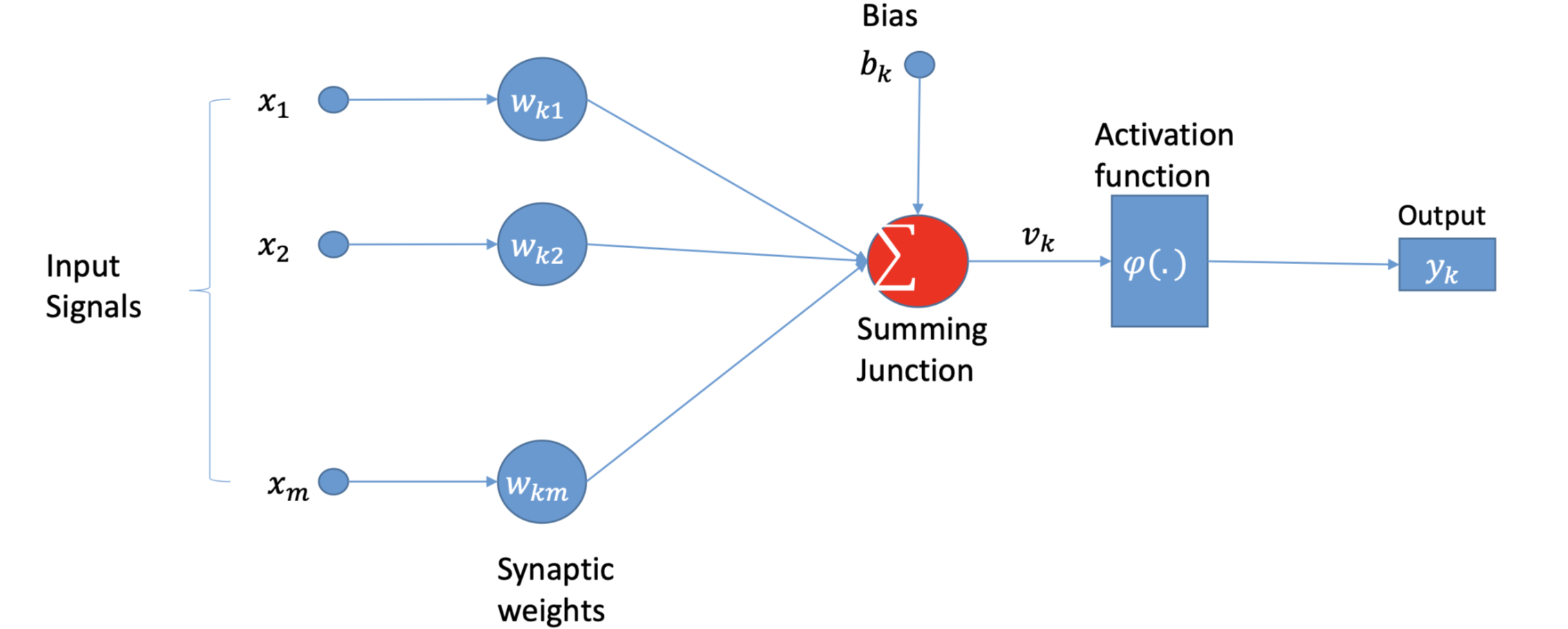
ANN structure.png

Figure 1 Perception structure

上图是一个感知机。x_m 代表输入，w_{km} 代表权重，求和后的结果会加上 bias，然后经过激活函数 Activation Function，最后得到输出。

bias相当于给线性变换加入了常数项。

相比于ANN，感知机的参数可以自动调整。

激活函数

Threshold Function

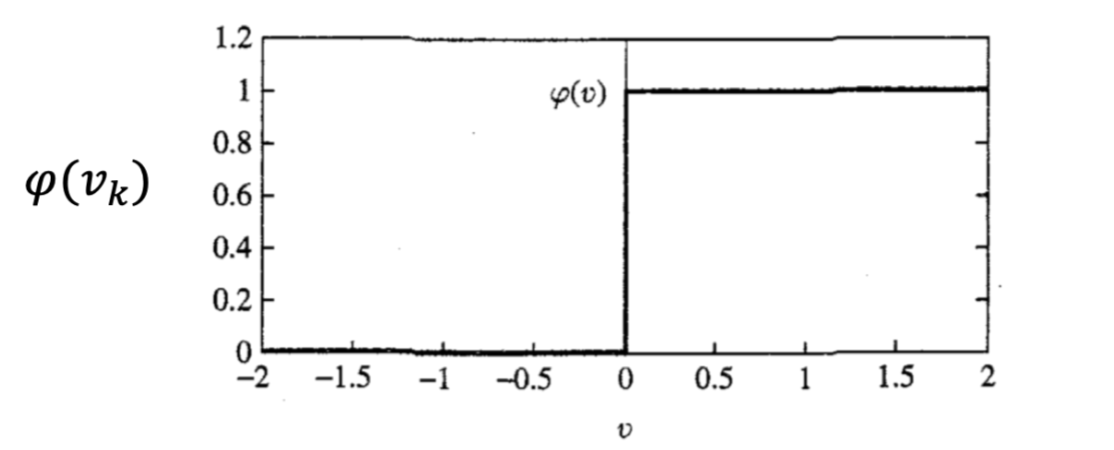
Threshold Function.png

Figure 2 Threshold Function

\phi(v) = \begin{cases}1\quad \text {if \textcolor{orange}{$v \geqslant 0$}} \\ 0\quad \text{if \textcolor{orange}{$v < 0$}} \end{cases}

这个激活函数不可微，因此不能用于梯度下降。

Piecewise-Linear Function

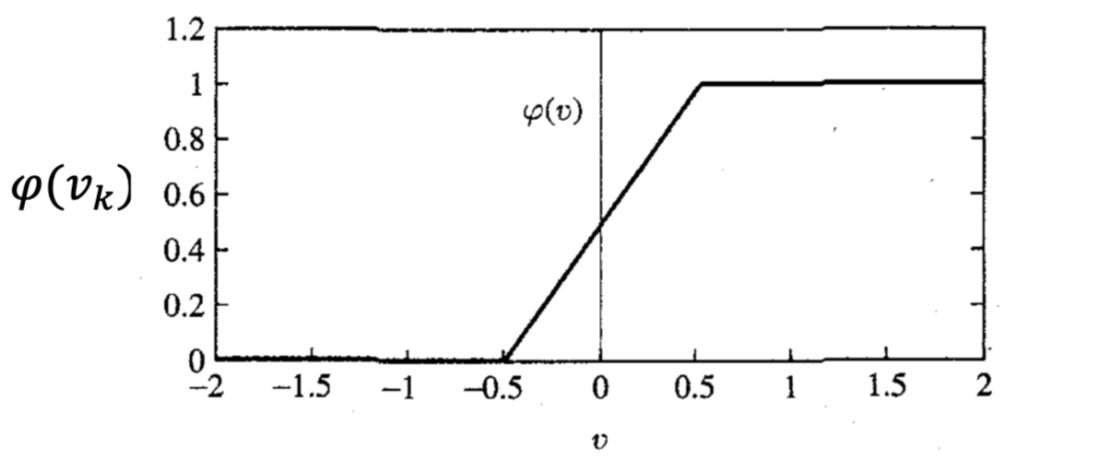
Piecewise-Linear Function.png

Figure 3 Piecewise-Linear Function

\phi(v) = \begin{cases}1\quad \text {if \textcolor{orange}{$v \geqslant +\frac {1}{2}$}} \\ v\quad \text{if \textcolor{orange}{$-\frac{1}{2} < v <+ \frac{1}{2}$}}\\ 0 \quad\text{if \textcolor{orange}{$v \leqslant -\frac{1}{2}$}} \end{cases}

Sigmoid

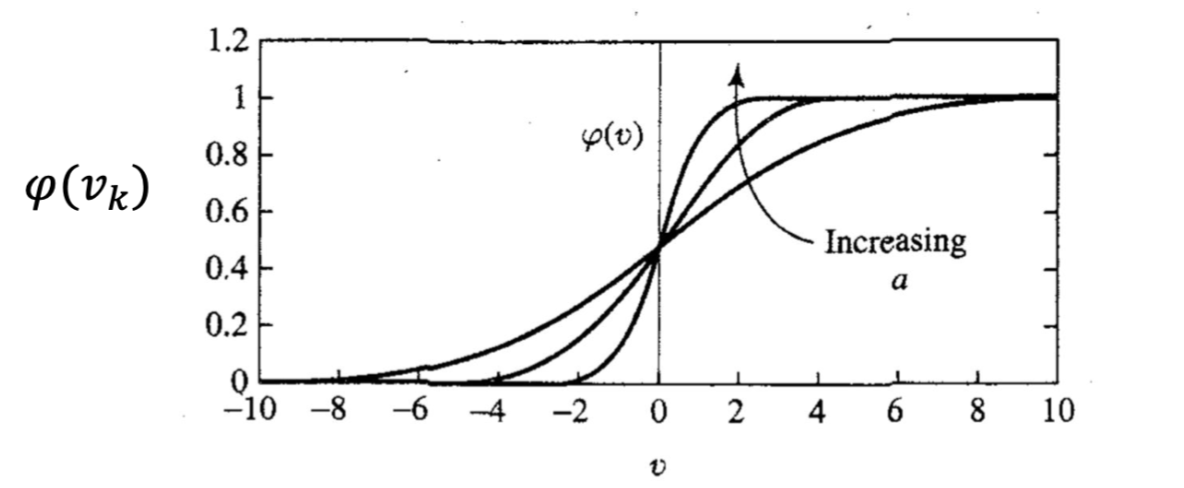
Sigmoid function.png

Figure 4 Sigmoid function

\phi(v) = \frac {1}{1+exp(-av)}

通过改变参数a，可以得到不同斜率的sigmoid函数，输出范围在0和1之间。

纠错学习

e_k(n) = d_k(n) - y_k(n)

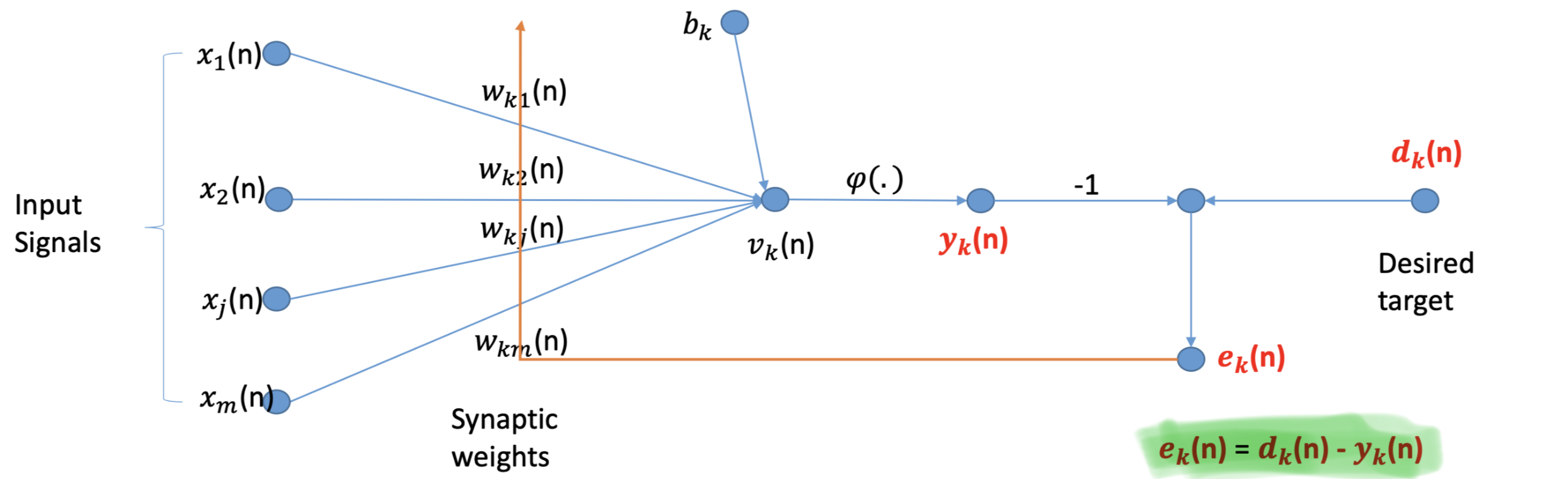
Error correction Learning.png

Figure 5 Error correction Learning

e_k(n) 可以作为一个反馈来修正输入的weight：
回归：\Delta w_{kj}(n) = \eta e_k(n)
分类：\Delta w_{kj}(n) = \eta e_k(n)x_j(n)

此处 \eta 是一个正常数，代表着学习率。对一个神经元的突触权重所做的调整与误差信号和有关突触的输入信号的乘积成正比。

对于学习率的选择，如果 \eta 太大，它可能不会收敛，如果太小，它将需要很长的时间才能达到最小值。

通过使用这种方法，我们能够进行纠正性调整，以使输出信号逐步接近预期响应。这一目标是通过最小化cost function：

\epsilon(n) = \frac{1}{2}e^2_k(n)

随着时间的推移，我们要做的是使我们训练数据集中的所有训练数据项的 cost function 最小化。此外，系统将达到一个稳定的状态，突触权重将变得稳定。

多层感知机，MLP

之前提到的单层感知机对简单的问题（回归和一些二元分类）来说效果不错，但是对于更复杂的问题来说，需要更复杂的网络。

多层ANN.png

Figure 6 多层感知机

站内导航

机器学习- 感知机 Perception