聚类

聚类是一种无监督的机器学习方法，它能使类似的对象从其他对象中分离出来。它是无监督的，因为我们没有给模型任何标签；它只是检查特征并确定哪些样本是相似的并属于一个群组。

常见的聚类算法有：

• 分层聚类算法（Hierarchical Cluster Analysis HCA）
• k-Means
• Expectation Maximization
• DBSCAN

分层聚类

分层聚类被分成两种类型：聚合型和分类型。

• 聚合型： 这是一种自下而上的方法：每个观测值都从它自己的聚类开始，随着层次的上升，成对的聚类被合并。
  最初，每个数据点被认为是一个单独的聚类。在每次迭代中，相似的聚类与其他聚类合并，直到形成一个聚类或K聚类。聚合型聚类的流程如下：

  1. 在开始时，让每个数据点成为一个聚类
  2. 计算距离/邻近矩阵
  3. 重复
  4. 合并最近的两个聚类
  5. 更新距离/邻近矩阵以反映新聚类与原始聚类之间的类似程度
  6. 直到只剩下一个聚类

• 分类型：这是一种自上而下的方法：所有的观测值都从一个聚类中开始，当人们向下移动层次时，会递归地进行拆分。

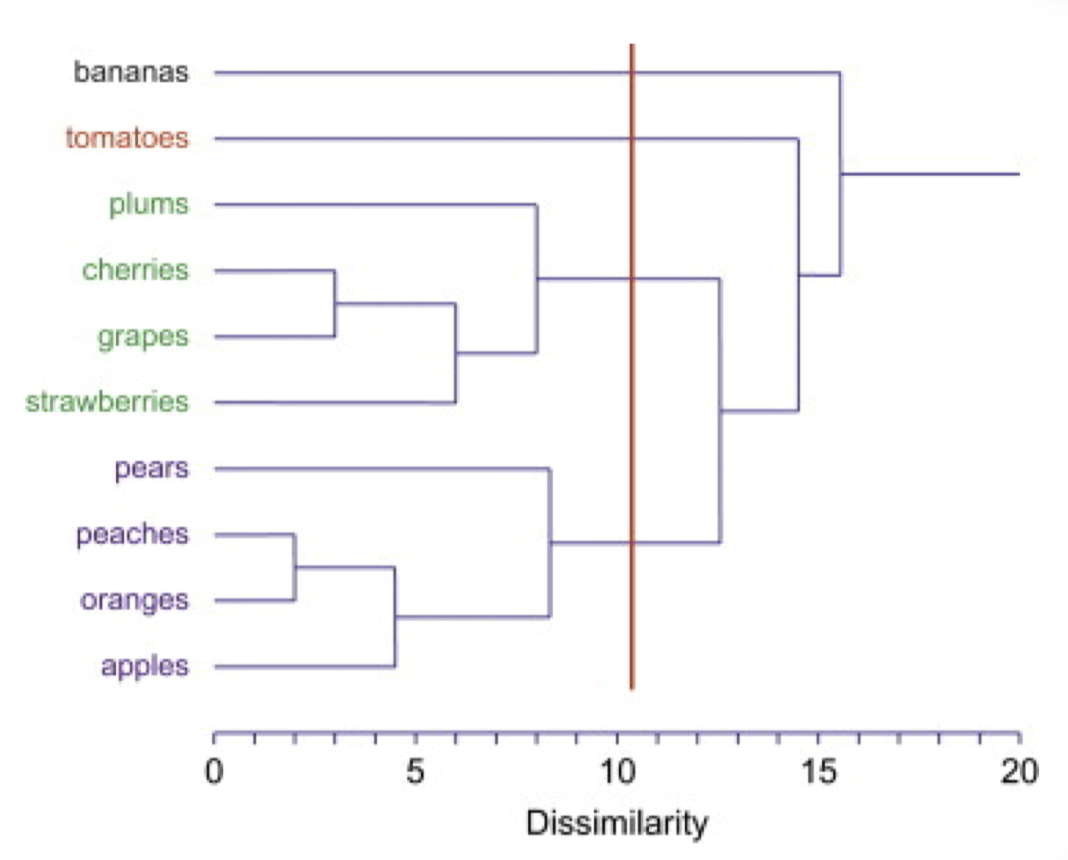
距离/邻近矩阵

距离的计算方式有很多种，平时在空间坐标系中，我们常使用的距离是欧几里得距离（Euclidean Distance），除此之外，还有曼哈顿距离，马哈拉诺比斯距离等，不同的距离计算方式，会影响聚类的结果，懒得用markdown敲公式了，直接放图。。。

合并的标准

公式中的d是所使用metric计算的距离。

• Min

相似性（C1，C2，C3） = 点 P_i 和 P_j 之间距离的最小值。因为 C1 中的 P_i 比 C3 中的 P_j 更接近 C2 中的 P_j ，所以 C1 和 C2 被合并。

只要两个聚类之间的差距不是非常大，这种方法就能分离出非椭圆形状。但是如果聚类之间存在噪音，MIN方法不能正确分离聚类。

• Max

相似性（C1，C3）= 点 P_i 和 P_j 之间的最大距离，C3 和 C1 合并到 C4 中，因为 P_i 和 P_j 的距离最远。

如果聚类之间存在噪音，Max方法在分离聚类方面表现良好，因为它找的是最远的点。然而 Max方法偏向于球状聚类（由于它寻找最远的点），并且总是倾向于打破大的聚类。

• 组平均和Ward方法

Ward法

• 中心距离法

计算两个聚类 C1 和 C2 的中心点，将两个中心点之间的相似度作为两个聚类的相似度。

分层聚类的复杂度

空间复杂度 O(n^2)
时间复杂度 O(n^3)
n为点的数量。

K-means

k-means聚类的目的是将n个观测值分为k个聚类，其中每个观测值都属于平均值最近的聚类。

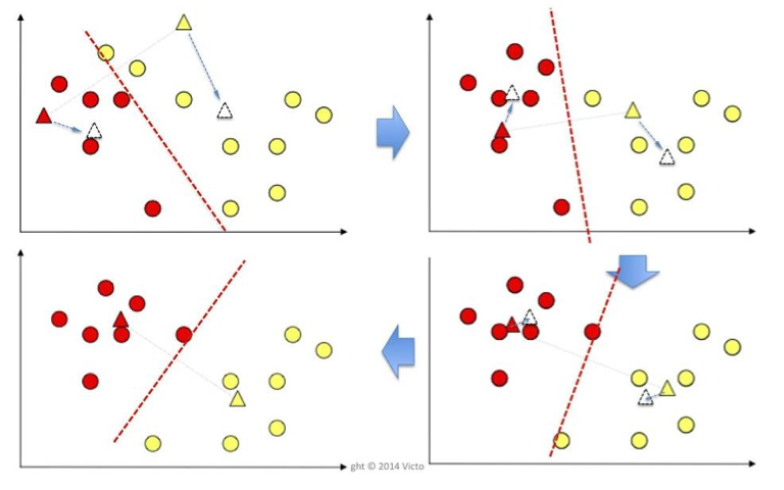
1. 给定一个初始k值。
2. 赋值：将每个观测值（每个圆圈）分配到平均数的欧几里得距离最小的聚类中，这在直觉上是 "最近的 "平均数
3. 更新：计算新聚类中观测值的新平均值（中心点）。
4. 重复：直到中心值不再变化（收敛）。

不同的初始中心点会明显的影响聚类结果，因为K-means也是一种贪心算法

K的确定

一般基于一些先验知识或常识。
要是没有相关经验，可以设定多个K值，并评估聚类的结果。