主成分分析
通常获取到的数据集都会有很高的维度，会给运算造成很大压力，所以需要降维，但是我们并不知道哪些数据更关键，因此引入了主成分分析 （Principal Component Analyses，PCA）的方法。
假设有个m维向量 \vec X，我们希望用 I个变量来保存它，如果简单地把 \vec X截成 I个变量那么会损失很多的数据。所以，我们想找到个线性变换 q，使得 A = X^Tq = q^T X。
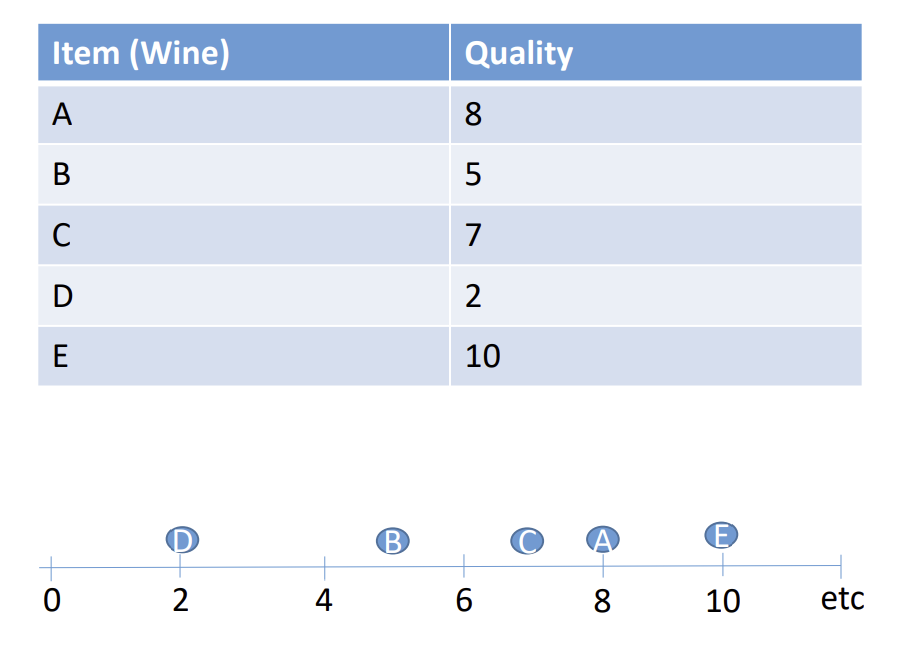
Figure 1 1-D数据
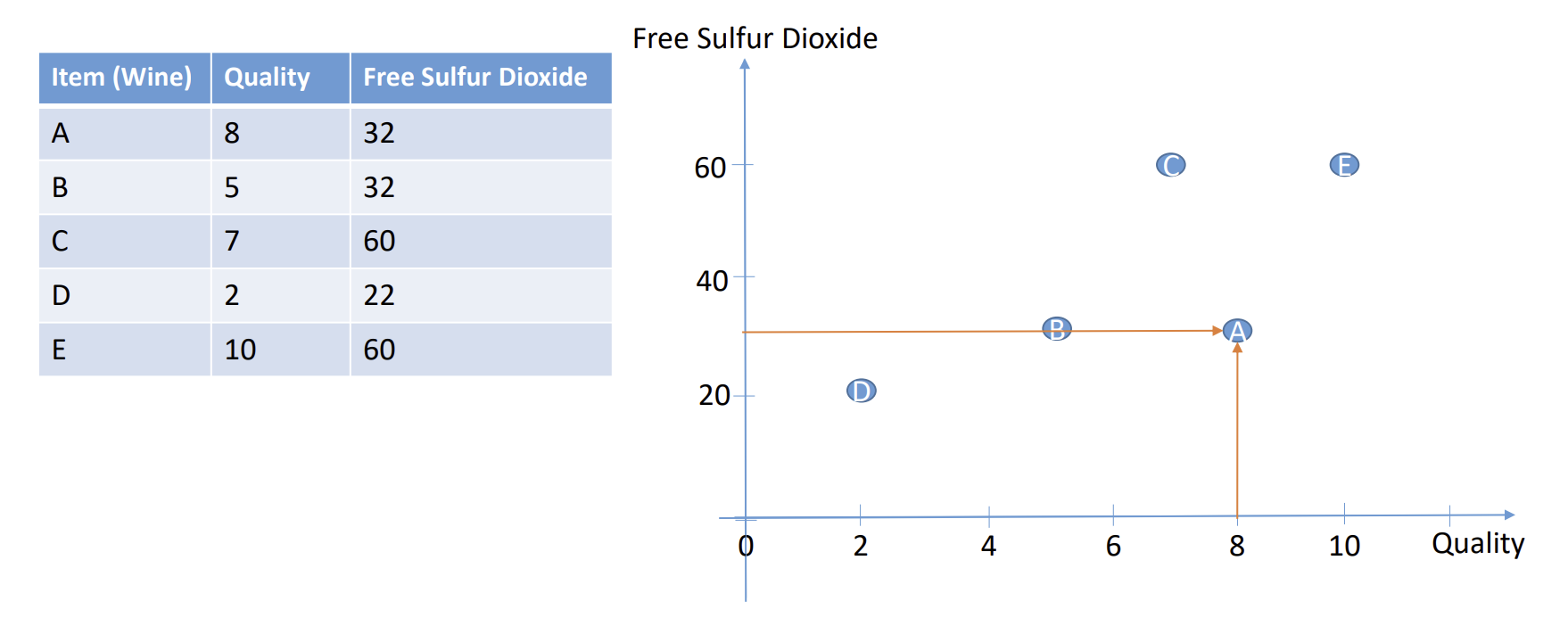
Figure 2 2-D数据
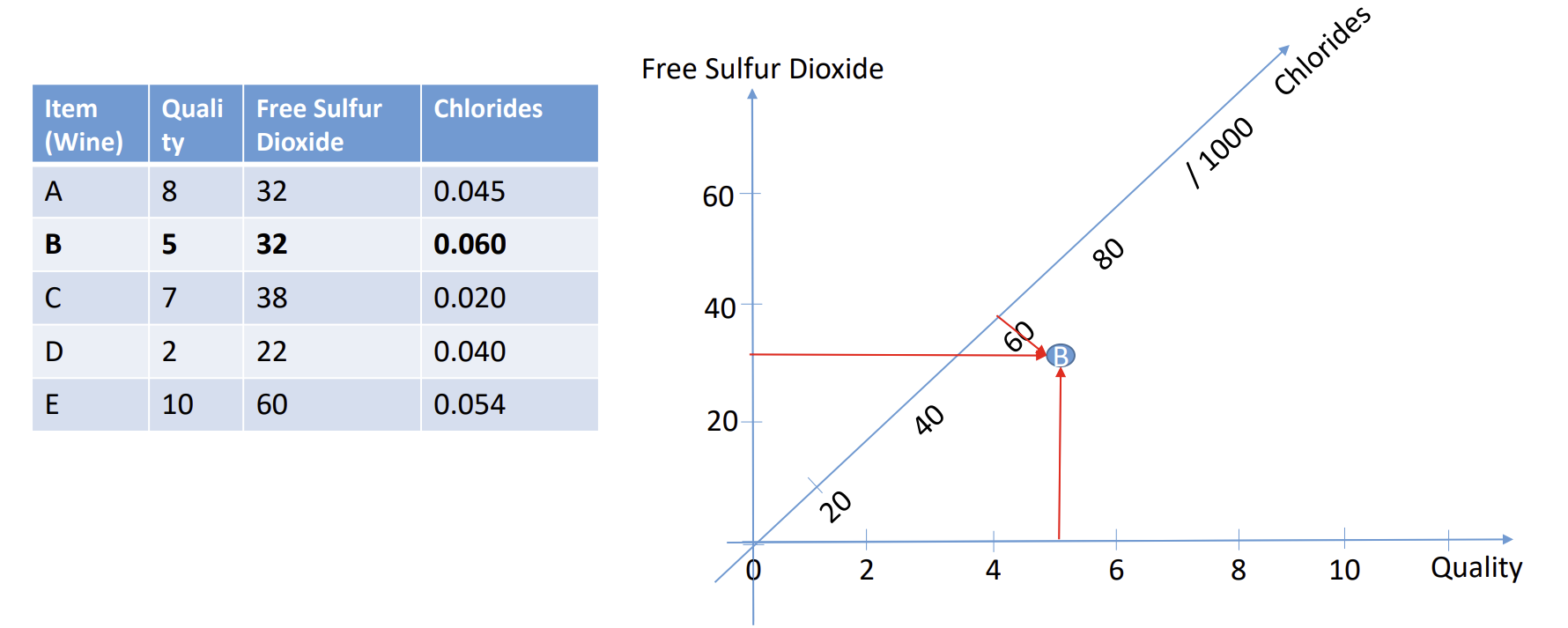
Figure 3 3-D数据
如果维度>3，就很难画出来了。
但是我们发现，如果旋转坐标轴，可以用2-D数据来表示3-D数据。为了能表达尽可能多的数据，需要找到旋转的特征向量 q（eigen vector）
这2条能够代表3-D数据的变量就被成为主成分（Principal Components），变化最大的线被称为PC1，另一条PC2。
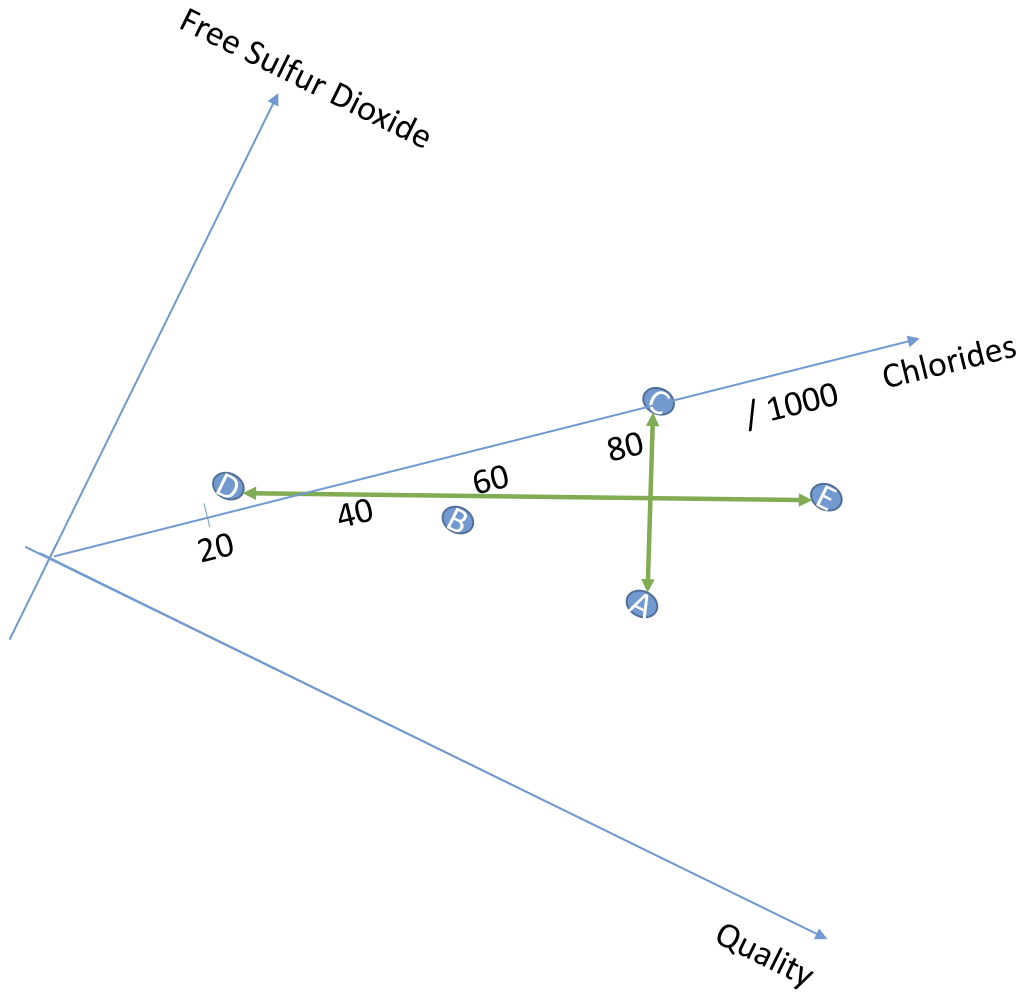
Figure 4 PC1
其中PC1最关键，因为它可以捕获到更多的数据集特征。
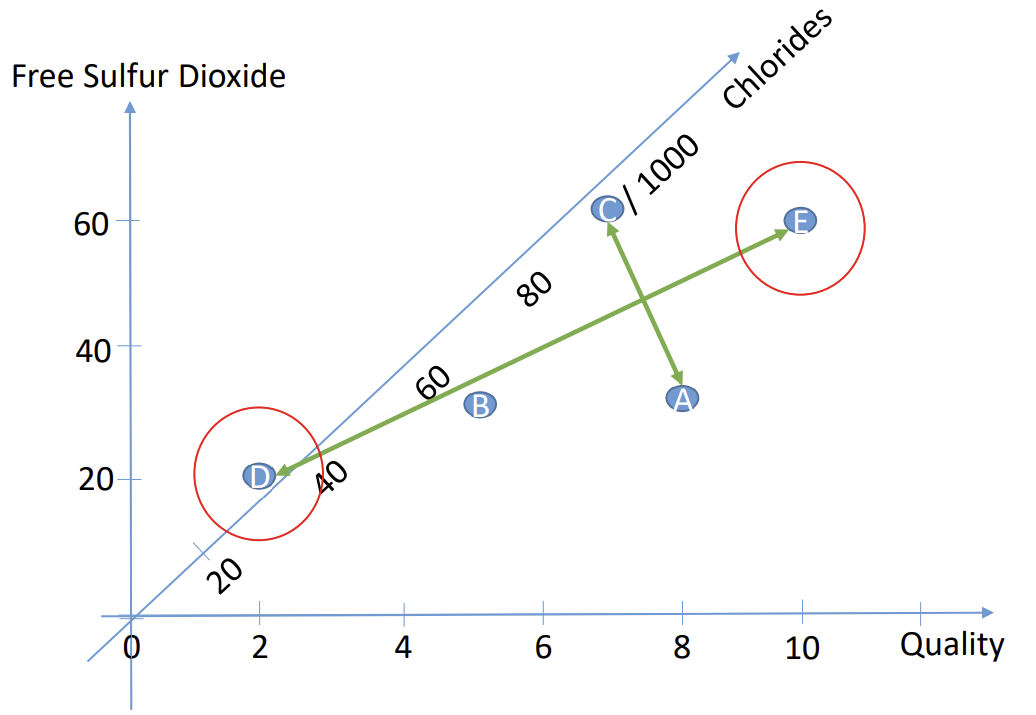
Figure 5 PCA
PC1的长度和方向由数据D和E决定，因此，这些点对PC有更大的影响。那些较远的点影响则比较小。同理，PC2的长度由A和C决定，因此这2个点对PC2的影响更大。
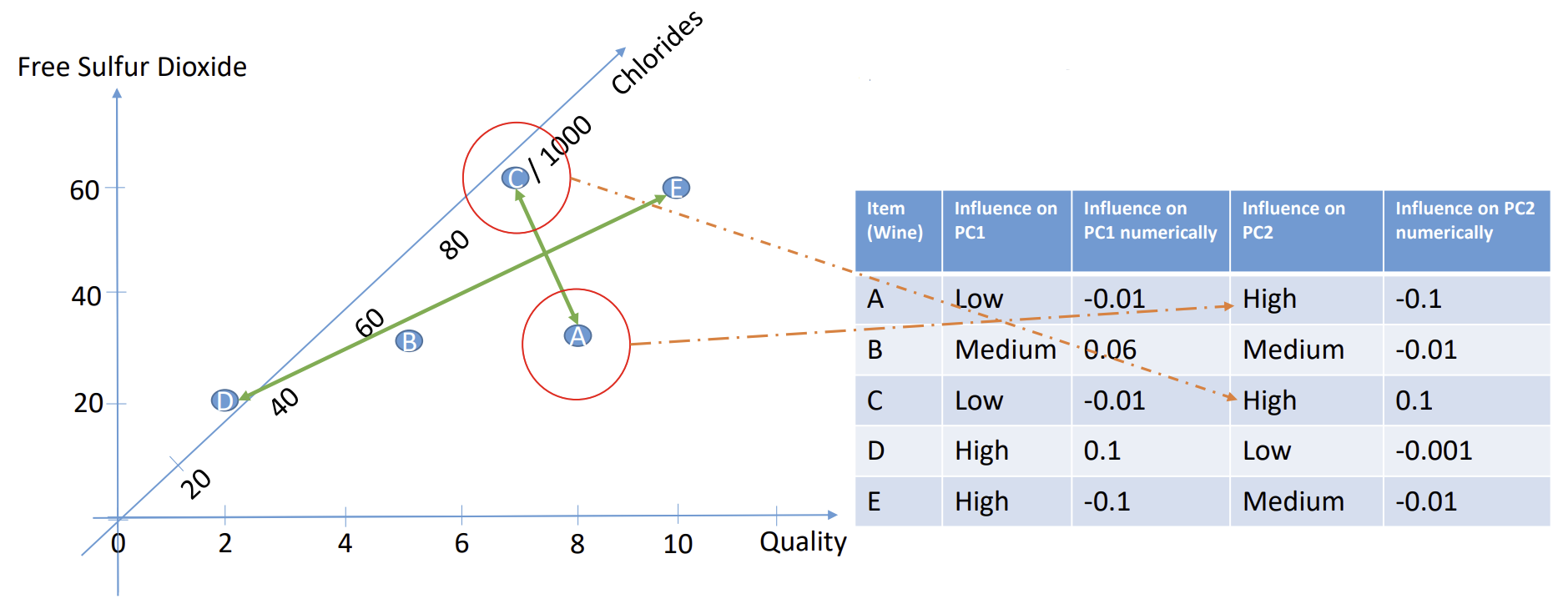
Figure 6 PC scores form
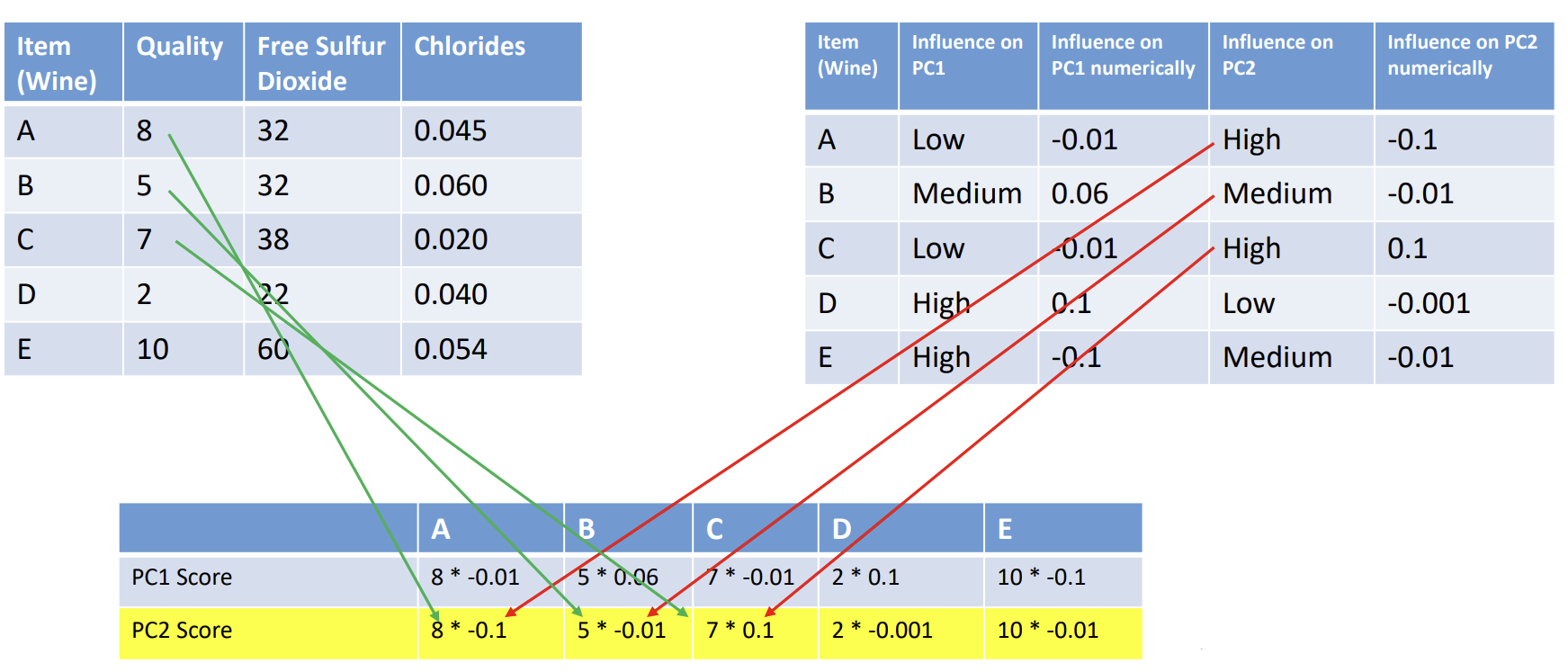
Figure 7 PC scores
影响的大小又被称为系数，权重或者负荷， 将标准化的原始变量乘以权重得出新的分数，称为成分分数。