傅里叶变换
傅里叶的原理说明:任何连续测量的时序或信号,都可以用不同频率的正弦波信号的无限叠加来表示。
在数学的角度来看,傅里叶变换算法利用直接测量得到的初始信号,用累加的方式来计算该初始信号中不同正弦波信号的频率,幅值和相位。
而从物理学的角度来看,傅里叶变换可以帮助我们将时域的信号转为频域来分析。有些在时域上很难分析的一些信号,在被转换到频域后,更容易找到其特征。此外,频谱也可以通过傅里叶变换得出。下图可以更好理解时域到频域的转换:
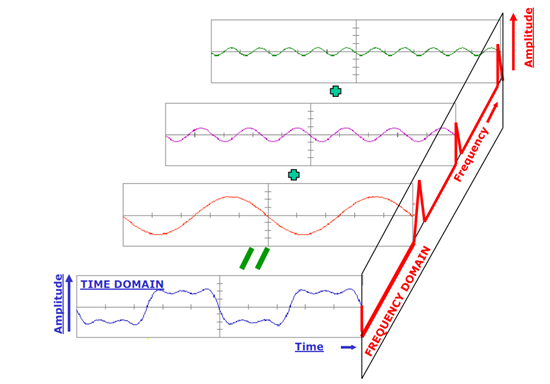
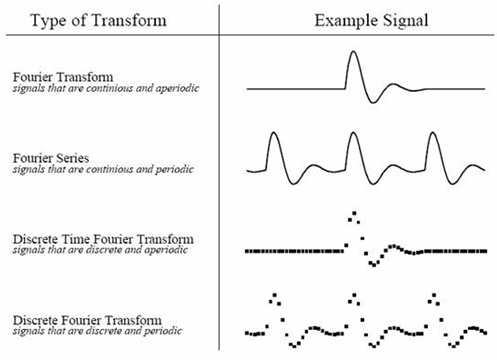
傅里叶变换的4种类型
- 非周期性连续信号傅立叶变换(Fourier Transform)
- 周期性连续信号傅立叶级数 (Fourier Series)
- 非周期性离散信号离散时域傅立叶变换(Discrete Time Fourier Transform)
- 周期性离散信号离散傅立叶变换 (Discrete Fourier Transform, DFT)
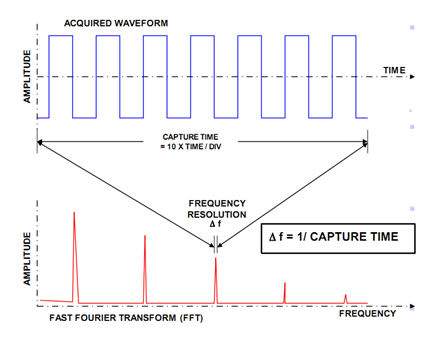
快速傅里叶变换
因为计算机只能处理离散数值信号,因此只有周期性离散信号离散傅立叶变换 (Discrete Fourier Transform, DFT) 适用。FFT也是DFT的一种快速算法。DFT运算过程如下:
其中,
X(k) - 频域的值
x(n) -时域的采样点
n - 时域采样点的序列索引
k - 频域值的索引
N - 采样点数量
对于在毕设中出现的平面曲线的descriptor, X(k) 和 Y(k) 分别代表 x 轴和 y 轴的坐标。
其中,
a(u) - 频域的值
s(k) - 复数表示的平面坐标点k
k - 点的索引
u - 频域值的索引
K - 曲线中的总点数
快在哪?
由公式可以看出,DFT后的输出包含与输入数量相同的采样点,但是有一半是冗余的,实际上只有 \frac N2 +1个点包含有用信息。
FFT相比DFT,原本时间复杂度为N^2的运算,变成了N\lg{N}。
快速算法实现举例
以下式为例
红色部分是在FFT中需要计算的分量,其他部分不需要计算 (简单的弧度关系 - e^{i\theta}),可以由红色部分推导得出:
变换前后信号的对应关系
原始信号幅值为 A,FFT结果的每个点(除第一个直流分量外),幅值就是 A 的 \frac N2 倍。直流(DC)分量,也就是第一个点 (0Hz),他的幅值是直流分量的 N 倍。
每个点的相位,就是该频率下的信号的相位。
从第一个点(直流分量)到最后一个点N表示采样频率,这个区间被 N-1 个点分成 N 等份,每个点的频率以此增加。F_n = (n-1) \times \frac {F_s}N。在某个点 n 处所能分辨的频率为 \frac {Fs}N 。F_s 为采样频率, N 为采样点数。
参考文献
[1] FFT的物理意义 avaliable @7/28/2022
[2] 数字图像处理中的傅里叶(DFT/FFT) avaliable @7/28/2022

