多目标跟踪算法
自动驾驶领域中的目标跟踪算法都是多目标跟踪算法，即MOT（Multiple Object Tracking），因为在这种场景中要跟踪的目标往往是多个，也有些文献会把MOT称为MTT（Multiple Target Tracking）。
MOT问题中并不是所有目标都会在第一帧出现，也并不是所有目标都会出现在每一帧。那如何对出现的目标进行初始化，可以作为跟踪算法的分类表征。常见的初始化方法分为两类：DBT（Detection-Based-Tracking）和DFT（Detection-Free-Tracking），主要区别在于初始化是使用模型检测到的结果还是手动初始化。
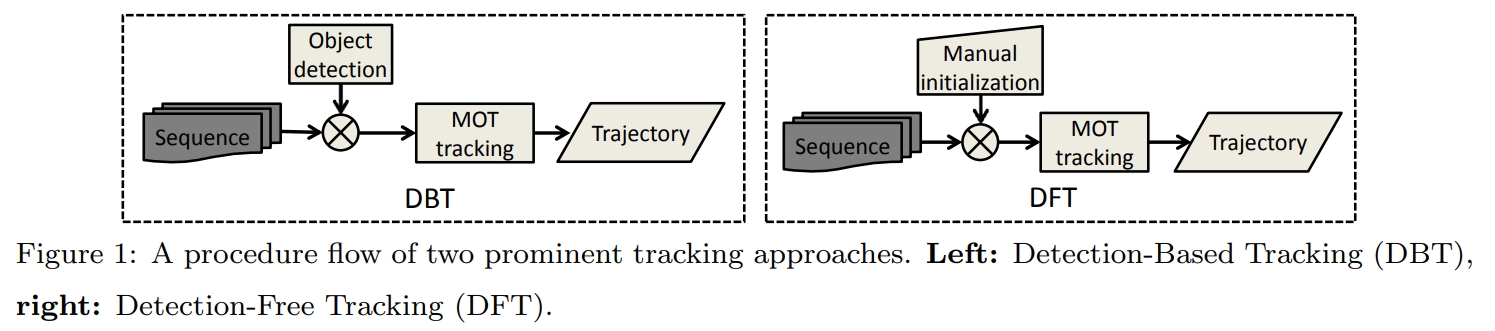
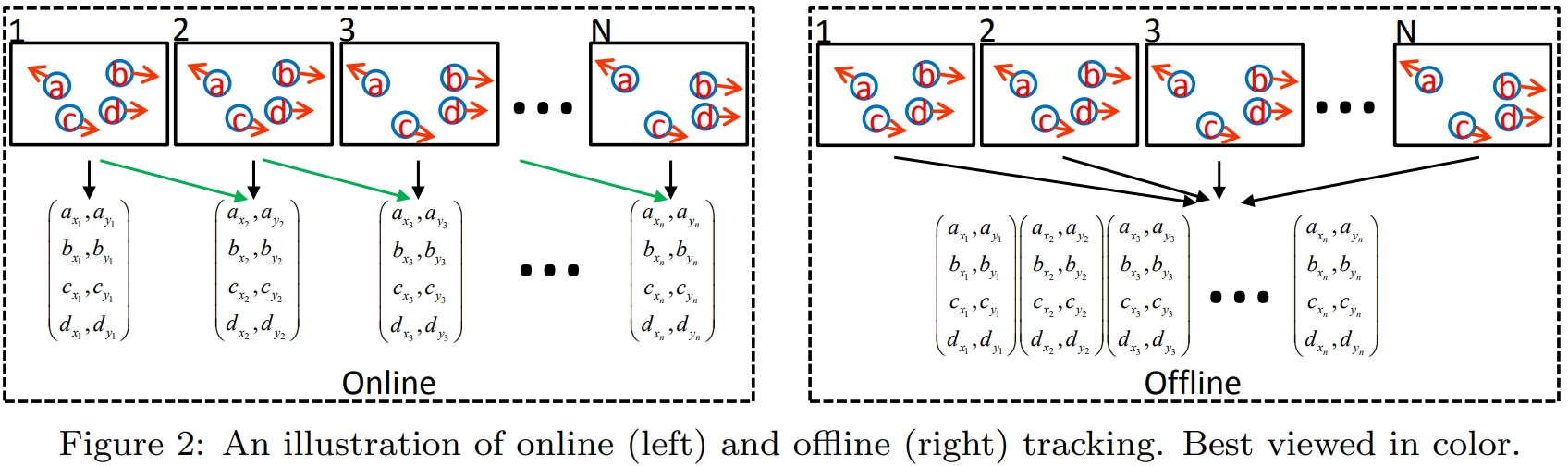
此外，MOT的处理模式也分为两类：Online和Offline。Online Tracking对视频帧进行逐帧处理，当前帧仅利用过去信息；Offline Tracking会利用前后视频帧的信息对当前帧进行目标跟踪，所以这种方法只适用于视频流，而不能用于实时的摄像头。
MOT算法就先简单介绍一下，后面再深入（主要是因为我也刚开始学...
目标匹配算法
当前主流的MOT框架都是DBT框架，这种框架依赖于数据关联算法，即目标间的匹配结果。良好的匹配结果能保证目标ID的连续性，由此可见目标匹配是MOT中的重要环节。当前目标匹配算法以偶图匹配为主。
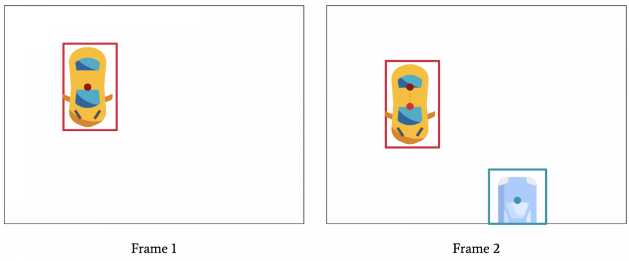
假设帧中只有一辆车，那么一直进行目标检测是OK的，下图黄色车辆ID会一直为1。
不过当帧中出现第二辆车，这种方法就寄了。
匈牙利算法
利用增广路找最大匹配的算法，就叫做匈牙利算法。匈牙利算法是专门用来求解指派问题的算法，通常用于求解二分图最大匹配。最大匹配即一个图所有匹配中，所含匹配边数最多的匹配。
简单描述一下：每个点从另一个集合里挑对象，没冲突的话就先安排上，要是冲突了就用增广路径重新匹配。重复上述思路，直到所有的点都找到对象，或者找不到对象也找不到增广路[8]。
二分图
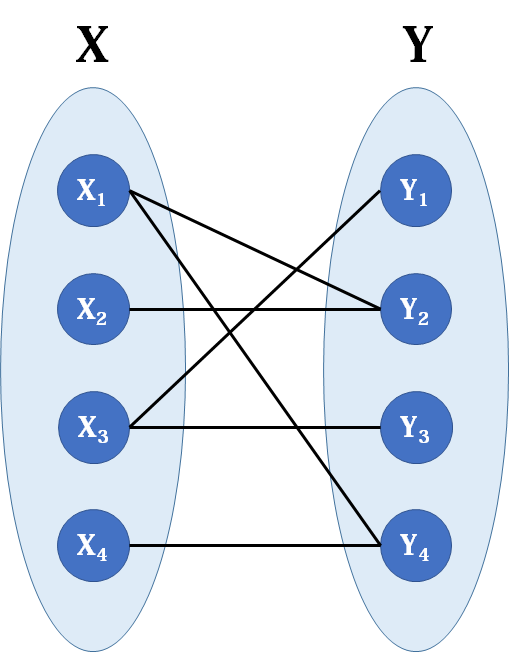
又称作二部图，是图论中的一种特殊模型。 设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边所关联的两个顶点i和j分别属于这两个不同的顶点集(i∈A, j∈B)，则称图G为一个二分图。下图就是一个典型的二分图：
下图乍一看不是一个二分图，其实也是一个二分图，转化一下，就会发现它其实还是一个二分图：
增广路和交替路
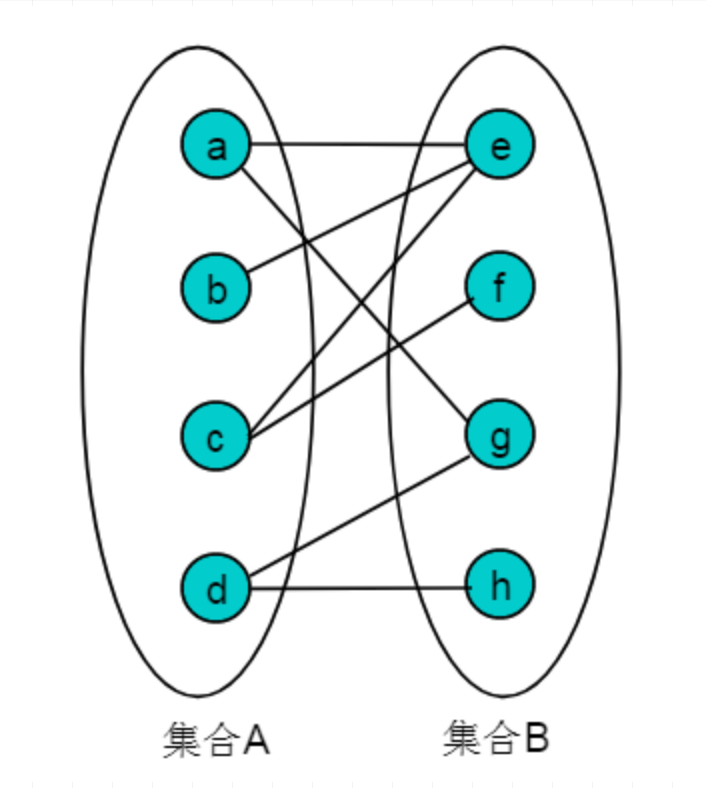
交替路：从一个未匹配点出发，依次经过非匹配边->匹配边->非匹配边形成的路径
增广路：从一个未匹配点出发，走交替路，如果途径另一个未匹配点（出发的点不算），则这条交替路称为增广路
增广路的性质：
P的路径长度必定为奇数，第一条边和最后一条边都不属于M，因为两个端点分属两个集合，且未匹配。
P经过取反操作可以得到一个更大的匹配M’。
M为G的最大匹配当且仅当不存在相对于M的增广路径。
算法流程
趣写算法系列之--匈牙利算法_匈牙利算法基本原理-CSDN博客 这篇博客写的非常好，没有公式，只用了几张图片，非常方便理解。
配对流程我们以下面这个二分图为例，图中蓝色连线代表的不是已匹配的边，这是一种初始匹配状态，所以蓝色连线是非匹配边。
开始匹配，先给A匹配，A和a会进行匹配，用红线将两者连起来，这条边变成了匹配边。但是接下来，B也想和a匹配，这就产生了冲突，交替路和增广路可以用来解决这个冲突。
找一条交替路，即依次经过非匹配边（蓝线）、匹配边（红线）。那么我们从B出发找交替路：
(非匹配边) (匹配边) (非匹配边)
B-------------------a-------------------A-------------------c
B和c都是未匹配的点，而且它们又是这条交替路的起点和终点。那么这条交替路就是增广路。现在进行一个取反操作，将上面这条增广路的匹配边变成非匹配边，非匹配边变成匹配边：
(匹配边) (非匹配边) (匹配边)
B-------------------a-------------------A-------------------c
就得到了下图，A和c匹配，B和a匹配：
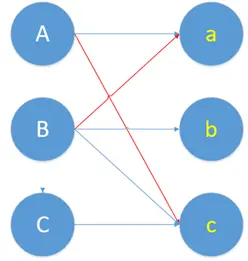
增广路最重要的特点是“起点&终点都是非匹配点”，这样就导致非匹配边比匹配边多了一条。由于增广路建立连接时，必须建立在两者有初始匹配的基础上，如果取反，就又得到了一条匹配边。取反的过程就是把原本匹配上的两个人拆散，给第三个人腾位置。
接下来对C进行匹配，C要和c匹配，又产生了冲突，把上述过程再进行一次：
（非） （匹） （非） （匹） （非）
C--------c--------A--------a--------B--------b
取反得到：
（匹） （非） （匹） （非） （匹）
C--------c--------A--------a--------B--------b
得到下图，ABC三个节点全部匹配完成，且找到了最大匹配。
KM（Kuhn-Munkres）算法
相比匈牙利算法，KM算法是带权二分图匹配。权重，可以理解为加了一种约束。KM算法用于求解二分图的最优匹配。如果一个图的某个匹配中，所有的顶点都是匹配点，那么它就是一个完美匹配。完美匹配一定是最大匹配，但并非每个图都存在完美匹配。
KM算法会建立一个图，其中有前一帧和当前帧的Node，然后计算两帧的Node间的距离，这个距离越小，代表两帧Node间更大概率的匹配。下图以Camra和LiDAR融合为例：
距离矩阵
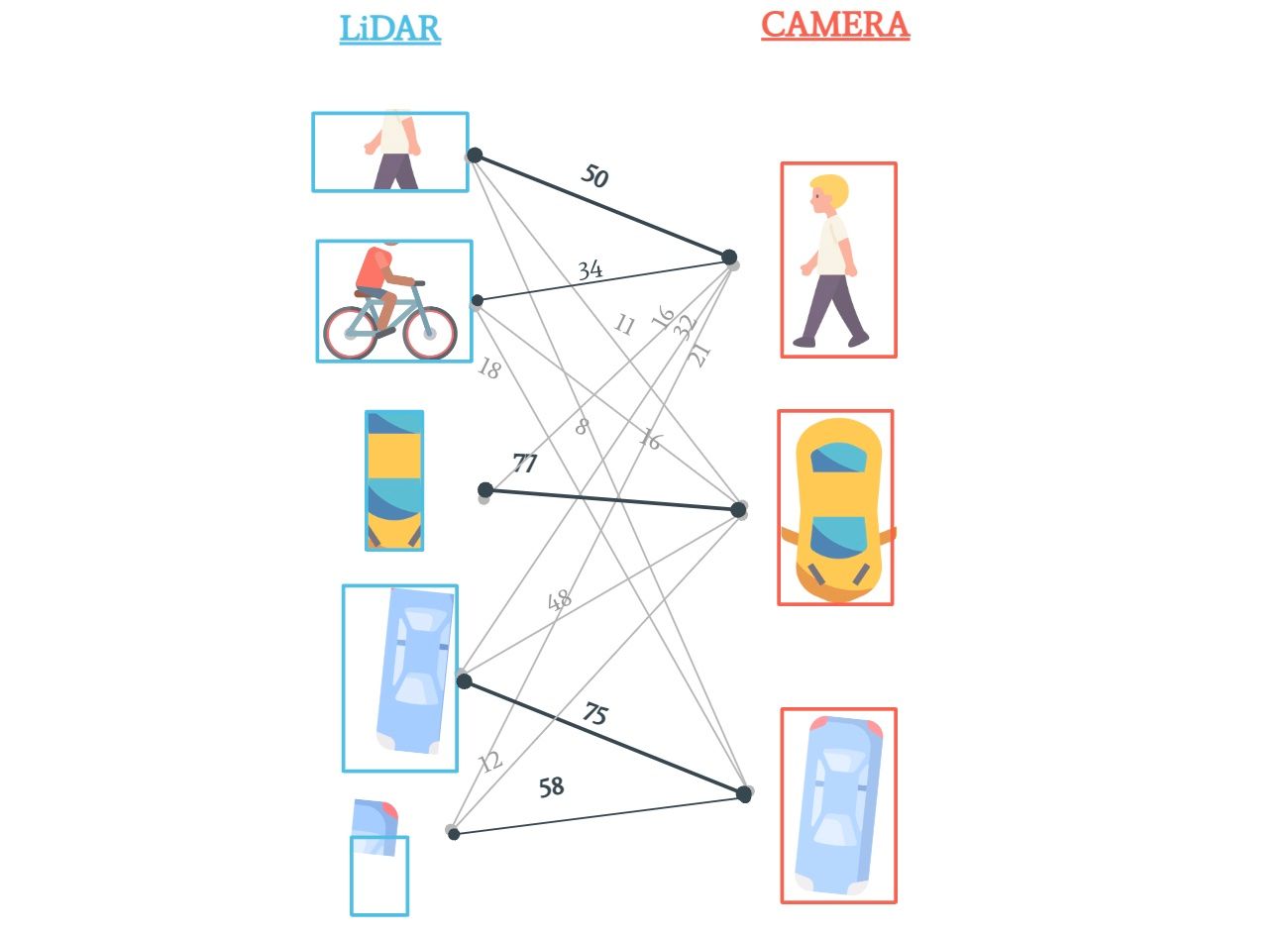
用一个距离矩阵为例：
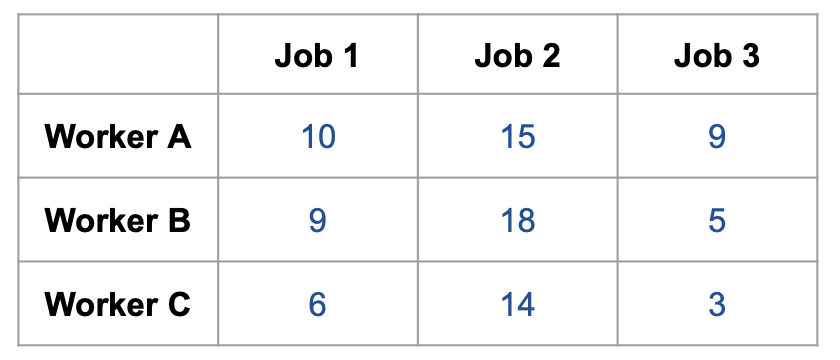
每行减去最小值，第一行减9，第二行减5，第三行减3：
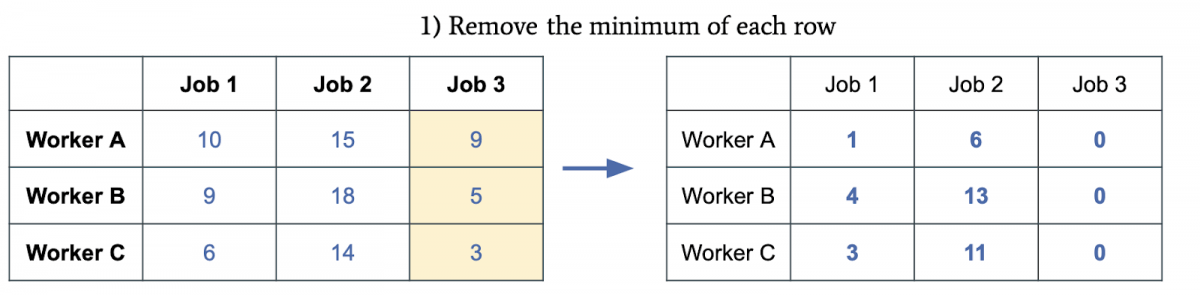
每列减最小值，第一列减1，第二列减6，第三列减0：
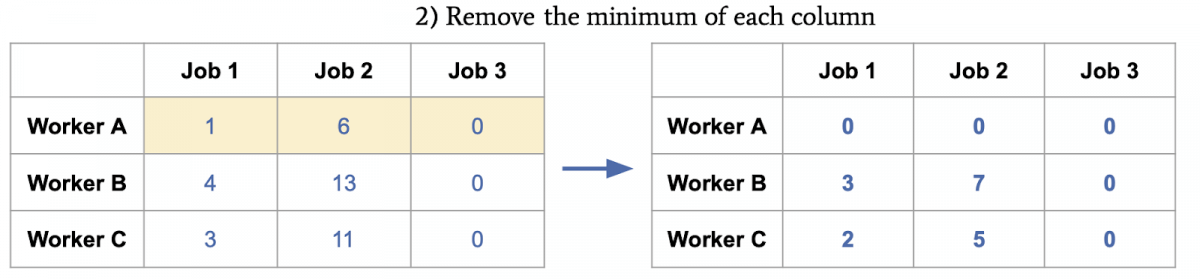
以最少数量的线，划掉所有零：
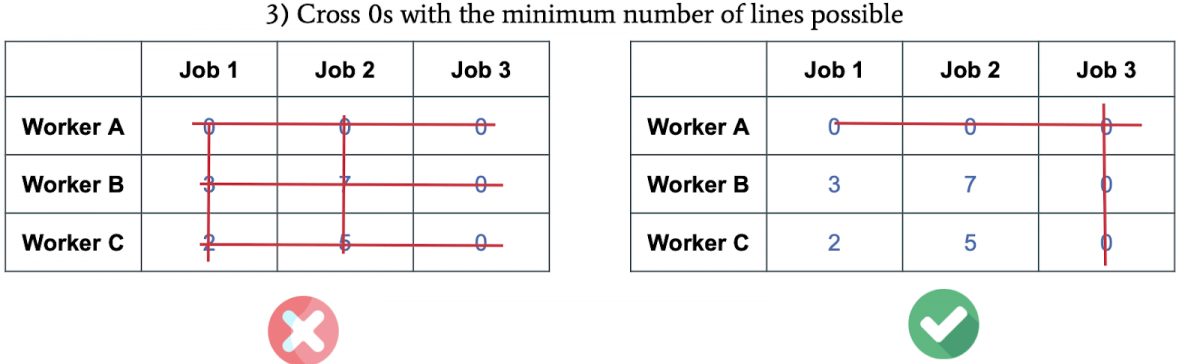
若 线数>=矩阵行列数，To Step 5；否则，在矩阵中减去最小值，若有0被交叉，则加上最小值：
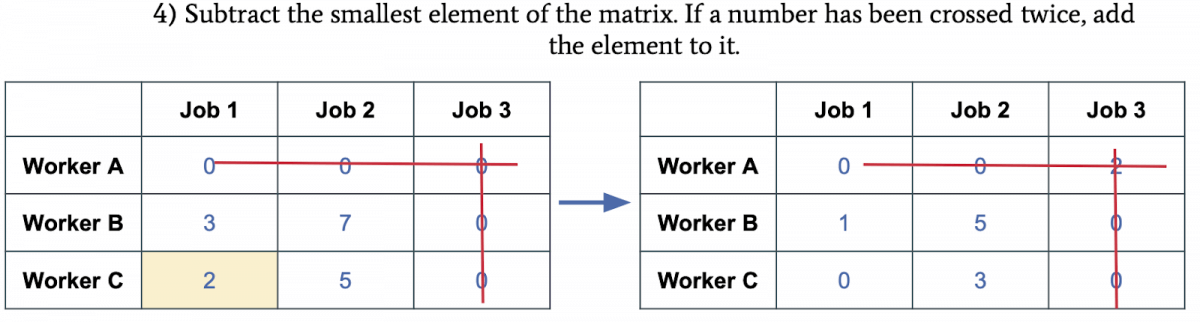
上图可以看出，剩下的[3, 7 ; 5, 2]全部减了2，同时线条交叉的部分加了2。再划线：
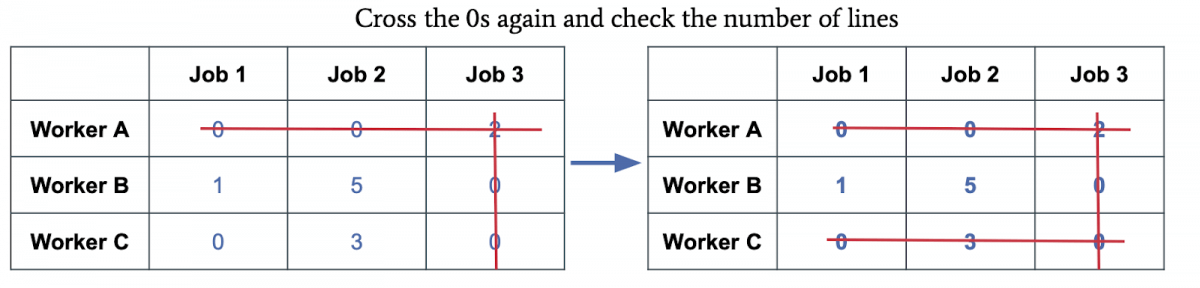
线数==矩阵行列数时，找只有一个0的行（按照作者所说，这种方法最终必定只有一行只有一个0），即第二行，WorkerB<->Job3，对应完成后删除该行。最终匹配为：
WorkerA<->Job2
WorkerB<->Job3
WorkerC<->Job1
距离的计算
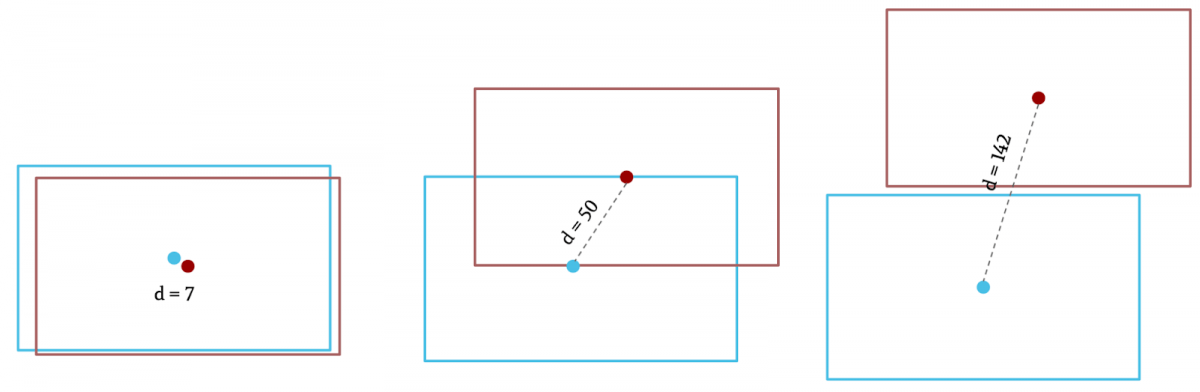
欧氏距离，即Bounding Box的中心点距离。但不能处理目标形状发生变化，或目标与其他目标重叠的情况。
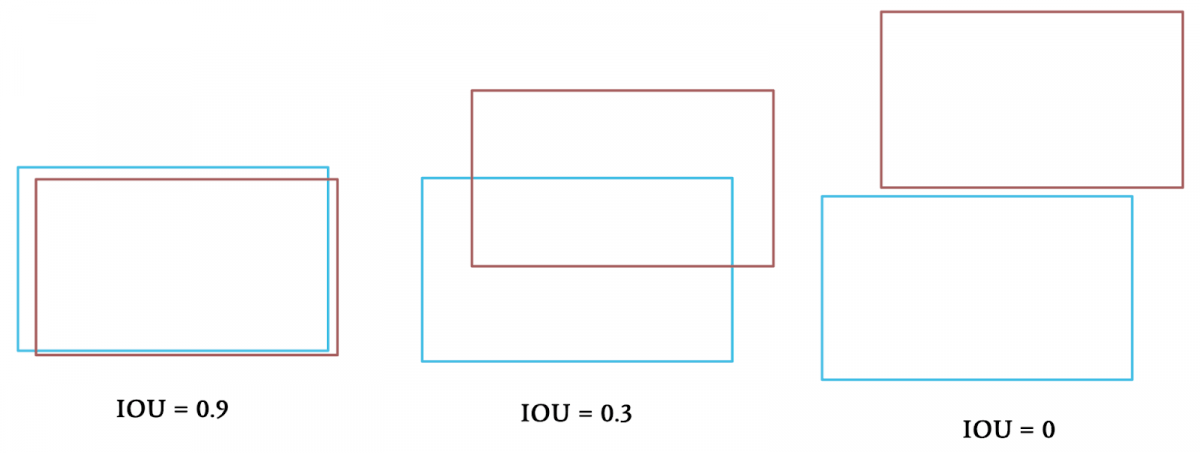
IOU，交并比。这种方法会让我们要解决的问题从寻找最小Distance变为寻找最大IOU。
Convolution Cost
使用CNN来查看Bounding Box内的图像，也是DeepSORT使用的算法。但是既然使用了CNN网络，会有更高的计算成本。相比SORT算法，DeepSORT算法会使用BBox内的外观信息。
Corner Case
若前帧出现了3个目标，后帧出现了4个目标。也就是从NxN问题，变成了NxM的问题。
解决办法是取整个矩阵最大值，填充新的列：
最大值和最小值
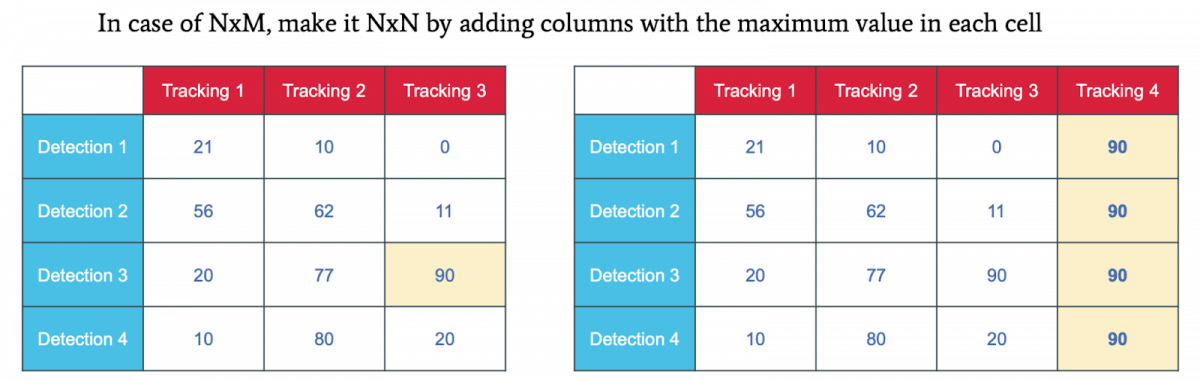
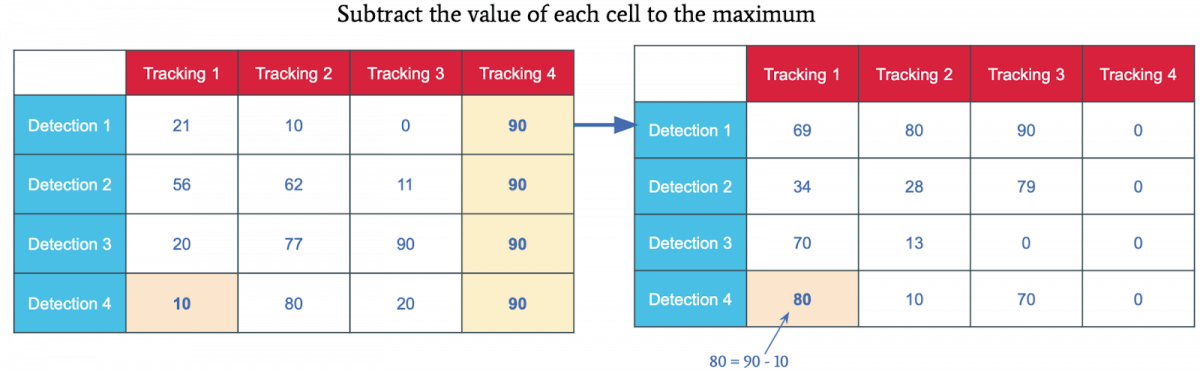
如果使用IOU，想进行最大IOU匹配；或者有相似性Cost，想进行最大相似性匹配。方法是取矩阵中最大值，并用这个最大值减去当前位置的值。
参考文章
[1] 多目标跟踪中的数据关联代码实践(上) | 见渊の博客 (huangpiao.tech)
[2] 【小白学习笔记】（一）目标跟踪-匈牙利匹配 - 知乎 (zhihu.com)
[3] 多目标追踪：DBT、DFT、基于Kalman和KM算法的后端优化算法、SORT/DeepSORT、基于多线程的单目标跟踪的多目标跟踪算法KCF_基于检测的跟踪范式(dbt)-CSDN博客
[5] Exactly how the Hungarian Algorithm Works (Self-Driving Cars Example) (thinkautonomous.ai)
[6] 趣写算法系列之--匈牙利算法_匈牙利算法基本原理-CSDN博客
[7] 【学习总结匈牙利算法到KM算法】_km匈牙利-CSDN博客
[8] 简单理解增广路与匈牙利算法 - 知乎 (zhihu.com)