Logo

菜单

MATLAB对点云数据(.pcd)的处理

FunnyWii
FunnyWii
发布于 2022-09-16 / 91 阅读
0
0

MATLAB对点云数据(.pcd)的处理

#MATLAB#Point Cloud

前言

本文内容是针对 .pcd格式的点云进行处理。
文中模型出自TU Wien采集的佛头模型[2]。

相关函数和算法

pcd格式点云文件读取

clear all
ptCloud = pcread('head1.pcd'); 
pcshow(ptCloud)

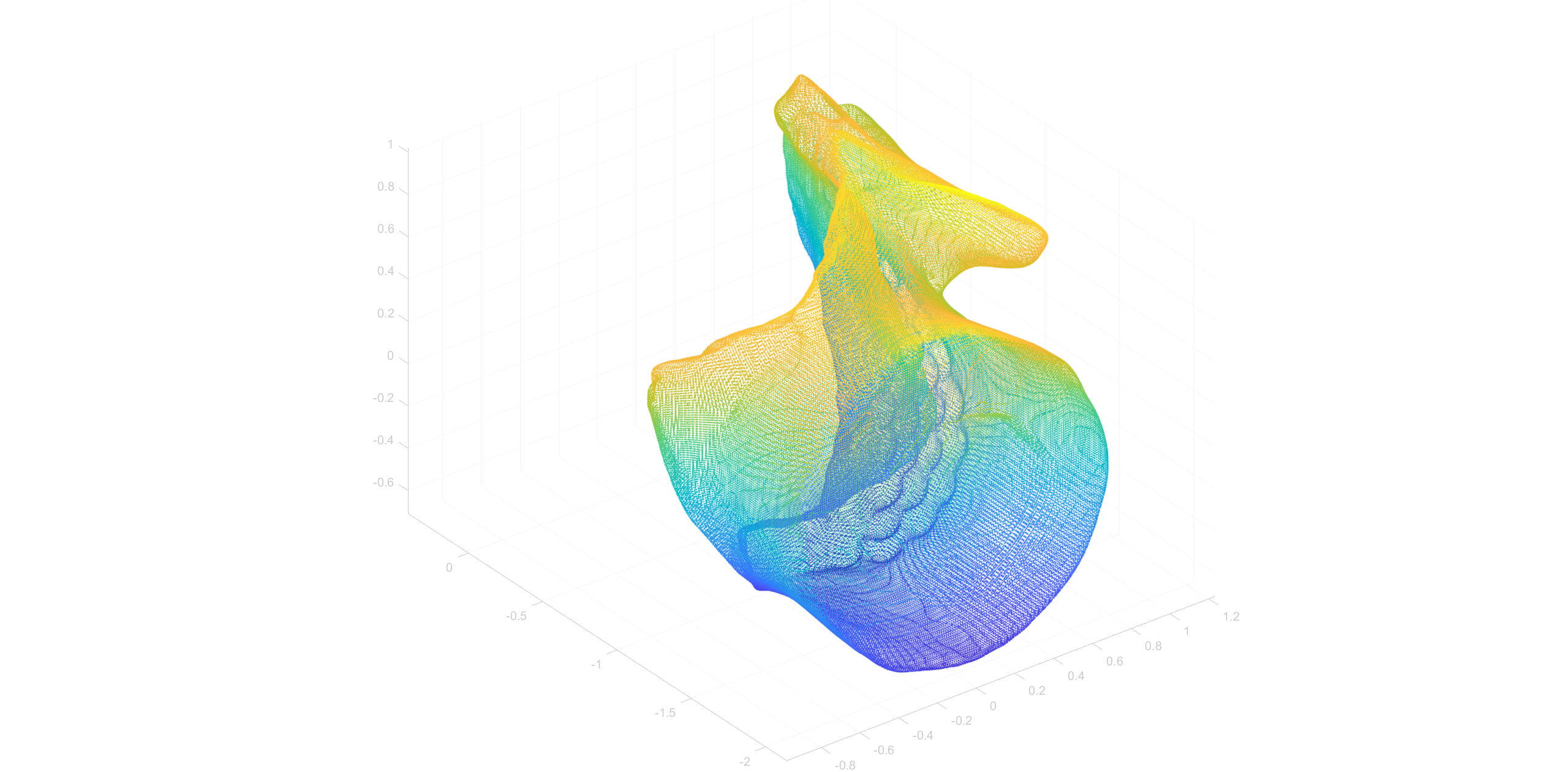
pcd1.png

Figure 1.1 佛头点云的可视化

对于 pcshow() 函数，默认显示点云为渐变色。且每个点的尺寸为默认为6。

如果想指定其RGB颜色：

% 随机RGB颜色
color = rand([1 3]);
pcshow(ptCloud.Location,color);

pcdrgb.png

Figure 1.2 显示点云为随机RGB颜色

如果想修改点的尺寸：

% 修改点的尺寸
pcshow(ptCloud.Location,r,'Markersize',0.1)

pcdsize.png

Figure 1.3 修改点云的点的尺寸

其中 ptCloud.Location，得到的是 ptCloud 中所有点的 x y z 坐标，是一个 n \times 3 的矩阵。

计算法向量

% 读取pcd
ptCloud = pcread('head1.pcd'); %读取点云
% 求法向量
normals = pcnormals(ptCloud);
% 点云x y z坐标
x = ptCloud.Location(:,1);
y = ptCloud.Location(:,2);
z = ptCloud.Location(:,3);
% 法向量 x y z坐标
u = normals(:,1);
v = normals(:,2);
w = normals(:,3);
% -------------------法向量可视化-------------------------
quiver3(x,y,z,u,v,w);
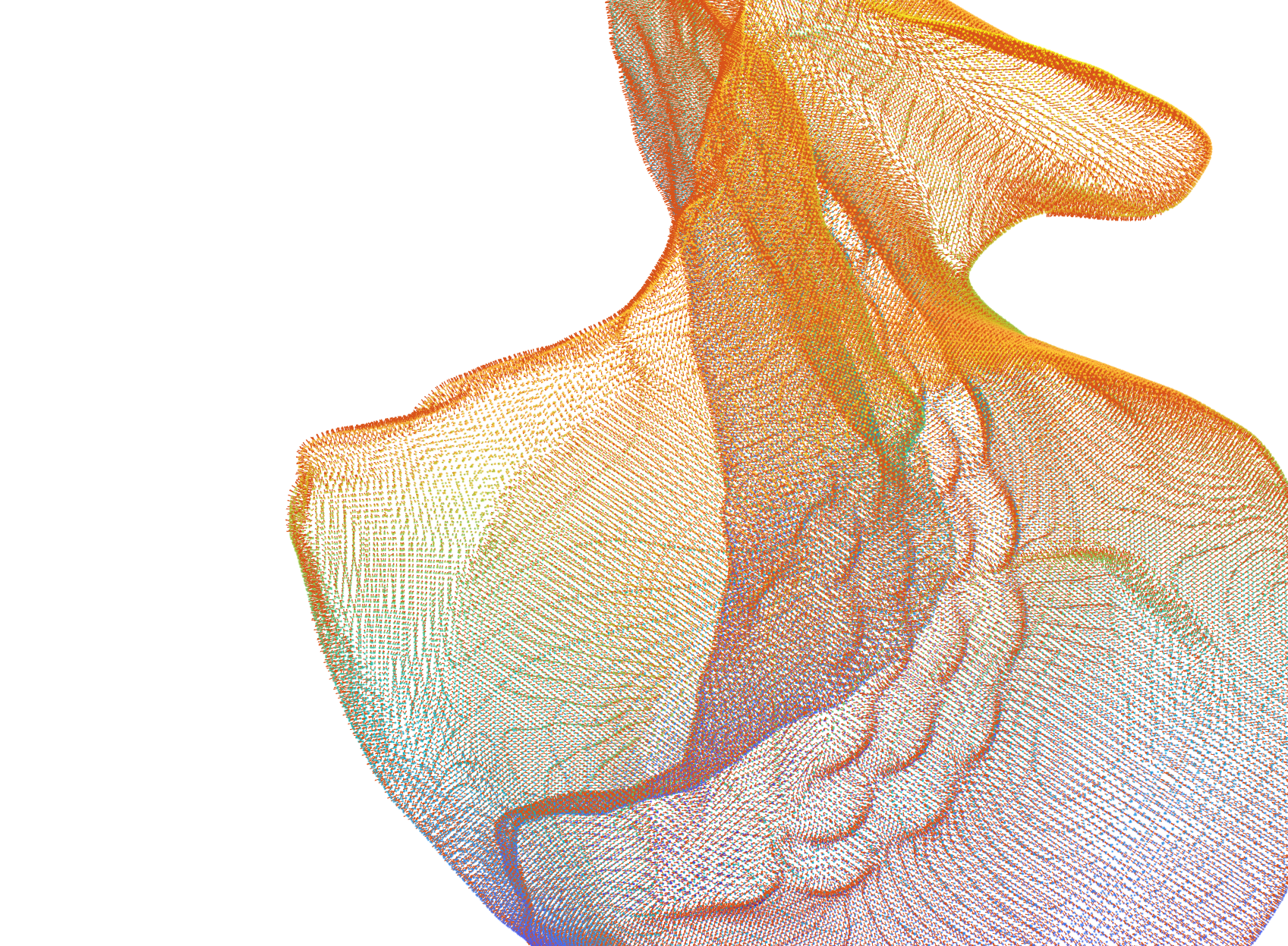pcdnormalvec1.png pcdnormalvec2.png
Figure 2.1 点云的法向量及其局部显示

计算曲率

点云的曲率一般指 1. 主曲率，2.平均曲率，3.高斯曲率
根据 B. He 等人提出的计算方法[1]，高斯曲率K和平均曲率H可以按照下列公式计算：

= \frac{r_{xx}{\cdot n\cdot r}_{yy}\cdot n\ -\left(r_{xy}\cdot n\right)^2}{2\left(r_x^2\cdot r_y^2-\left(r_x\cdot r_y\right)^2\right)}
\frac{r_x^2\cdot r_{yy}\cdot n-2r_x\cdot r_y\cdot r_{xy}\cdot n+r_y^2\cdot r_{xx}\cdot n}{2\left(r_x^2\cdot r_y^2-\left(r_x\cdot r_y\right)^2\right)^2}

之后，主曲率C_{min}以及C_{max}便可以求出：

{min}=H-\sqrt{H^2-K}
{max}=H+\sqrt{H^2-K}

其中，r_{xx}等变量代表点云表面的偏导

计算平面度

这个计算方法在1997年由Westin提出[4]，起初用来拟合平面。公式为：

planarity=\frac{2\left(\lambda_2-\lambda_3\right)}{3{(\lambda}_1+\lambda_2+\lambda_3)}

此处的 \lambda 为点云中的某个点，及其邻域构成的 n \times 3 矩阵的特征值

P = [x y z];
 planarity = zeros(length(x),1); 
 K = 50;
for i = 1 : length(x)             % 遍历点云中的每个点  
   point = P(i,:);
   [indices,dists] = findNearestNeighbors(ptCloud,point,K,'sort',true); %knn搜索
   % 1. 获取近邻点坐标
   nnpoint=P(indices,:);
   % 2. 计算区域的质心
   centroid = mean(nnpoint,1);
   % 3. 去质心
   deMean = bsxfun(@minus,nnpoint,centroid);
   % 4. 协方差矩阵
   H = 1/length(indices)*(deMean'*deMean);
   % 5. 奇异值分解计算特征值
   s = svd(H);
   % 6. 计算平面度
   planarity(i) = 2*(s(2)-s(3))/3*sum(s);
end
% -------------------按平面度大小进行颜色渲染-------------------------
scatter3(x,y,z,3,planarity,);

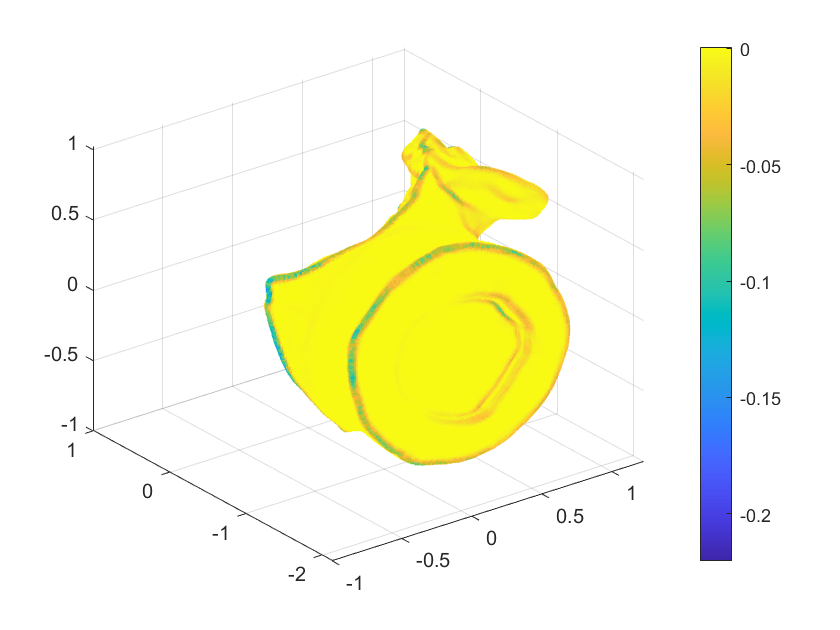
pcdplanarity.png

Figure 3.1 点云平面度

参考文章

[1] B. He, Z. Lin, and Y. Li, "An automatic registration algorithm for the scattered point clouds based on the curvature feature," Optics & Laser Technology, vol. 46, pp. 53–60, 03/01 2013, doi: 10.1016/j.optlastec.2012.04.027.
[2] Tu Wien "3D models are courtesy by Vienna University of Technology." https://www.geometrie.tuwien.ac.at/ig/3dpuzzles.html (accessed Sep.12, 2022).
[3] 点云侠, "matlab 计算点云的面状指数" https://blog.csdn.net/qq_36686437/article/details/124325407(accessed Sep.15, 2022).
[4] C.-F. Westin, "Geometrical diffusion measures for MRI from tensor basis analysis," Proc. ISMRM'97, 1997.

关于机器视觉(Machine Vi...
MATLAB对点云数据(.ply)的处理

评论