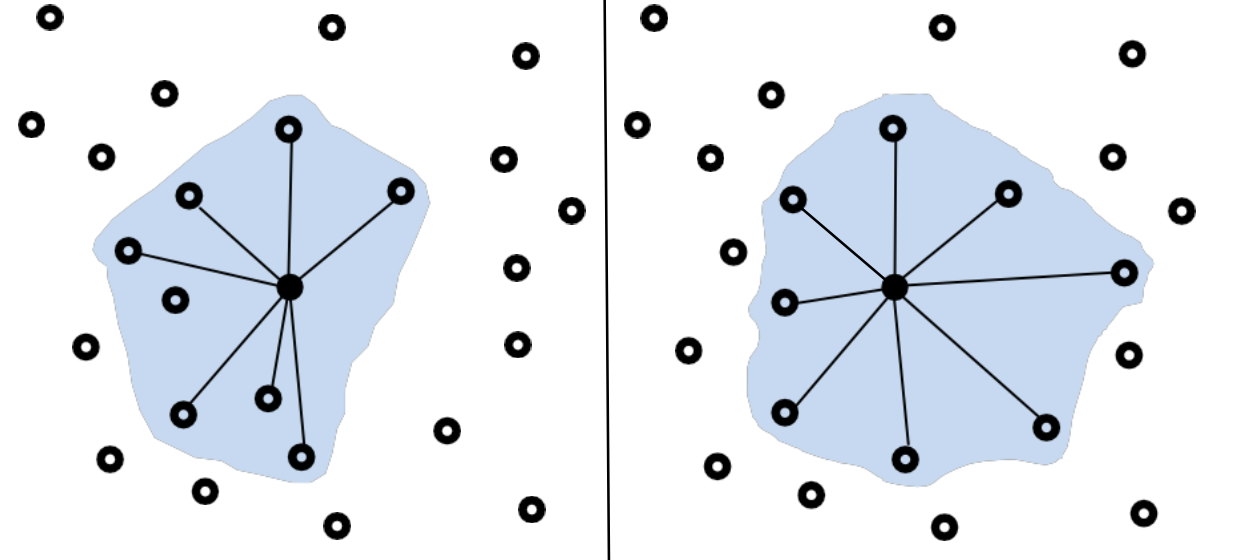
同质邻域
对于点云文件,因为缺乏分析公式的缘故,导致曲率计算比较复杂。
伞曲率使用K- NN算法,找到某个点的8个最近的相邻点,这8个点不仅要考虑最近距离,而且还考虑方向,这些点组成一个伞状区域。此区域被称为同质邻域(homogeneous neighborhood)。
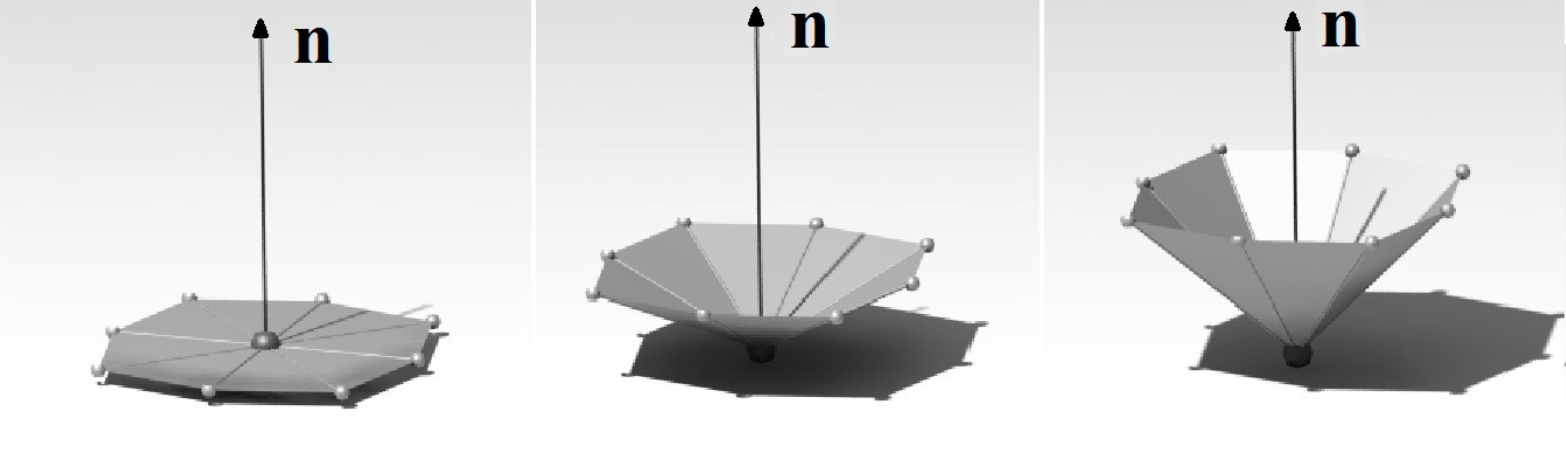
伞曲率
曲率是可以用来描述表面几何属性的不变特征。在点云表面处处光滑的情况下,任何局部邻域都可以很容易的求出曲率。然鹅,点云表面都不会太光滑。因此一个好的方法是在点及其周围8个点组成的邻域拟合一个平面。假设 k_{um} 为点 p 处的伞曲率。
k_{um} = \sum_{i=1}^8 ABS(\frac{N_i -p}{|N_i - p|}\cdot n)
其中 p 为某个点
N_i 为 点 p的同质邻域的第i个点
n 为在点 p 的法向量