登录
机器学习 - 正则化和优化器(Regularisation and Optimisers)
  算法   Machine Learning

机器学习 - 正则化和优化器(Regularisation and Optimisers)

 次点击
 25 分钟阅读

当模型可调节参数（自由度）过多时，容易学习到训练数据中的噪声，进而出现 “过拟合”（训练集误差小、测试集误差大）。因此要对模型的参数引入某种限制，在训练过程中避免过拟合。。

正则化通过在损失函数中加入参数惩罚项，约束参数规模，迫使模型优先学习数据的通用规律，而非噪声。

范数

在正式进入正则化的学习之前，先了解一下范数的概念。

范数的本质是对距离的抽象推广，一个函数 ​\|\mathbf{*}\|是范数，必须满足以下条件：

  1. 非负性：​\|\mathbf{x}\| \geq 0；
  2. 零向量特征：​\|\mathbf{x}\| = 0 \iff \mathbf{x} = \mathbf{0}（​\mathbf{0}为零向量）；
  3. 正齐次性：​\|\alpha \mathbf{x}\| = |\alpha| \cdot \|\mathbf{x}\|；
  4. 三角不等式：​\|\mathbf{x} + \mathbf{y}\| \leq \|\mathbf{x}\| + \|\mathbf{y}\|

向量范数中​L_p范数最为常见，定义为：

\|\mathbf{x}\|_p = \left( \sum_{i=1}^n |x_i|^p \right)^{\frac{1}{p}}

最常见的几种​L_p范数有：

  • L1范数，对应曼哈顿距离，L1范数是向量各个分量绝对值的和。
\|\mathbf{x}\|_1 = \sum_{i=1}^n |x_i|
  • L2范数，对应欧几里和距离，向量各分量平方和的平方根。L2范数应用最广，如果直接省略了下标变成​∥x∥的形式，一般是指L2范数。
\|\mathbf{x}\|_2 = \sqrt{\sum_{i=1}^n x_i^2} = \sqrt{\mathbf{x}^T \mathbf{x}}
  • L∞范数，对应车比雪夫距离，是向量各分量绝对值的最大值。
|\mathbf{x}\|_\infty = \max_{1 \leq i \leq n} |x_i|
  • L0范数，严格意义上来说，不符合范数定义，所以应该叫L0伪范数。定义为向量中非零元素的个数。
\|\boldsymbol{x}\|_0 = \sum_{i=1}^n \mathbb{I}(x_i \neq 0)

其中​\mathbb{I}(\cdot)为指示函数，当​x_i \neq 0时，​\mathbb{I}(x_i \neq 0) = 1，否则为​0。

正则化方法

常见的正则化方法：

  • Ridge Regression，也被称作L2 Regression，通常作为默认的正则化手段使用。
  • Lasso Regression，也被称作L1 Regression
  • Elastic Net

上述正则化方法，都有一个正则项（regularization term）被添加到 ​cost function 中。

L2 Ridge Regression

在原有损失函数的基础上，加入参数的平方和惩罚项，惩罚项系数 ​\alpha 为正则强度。

​cost function 就变成了：

J(\theta)=MSE(\theta)+\alpha\frac{1}{2}\Sigma^n_{i=1}\theta_i^2

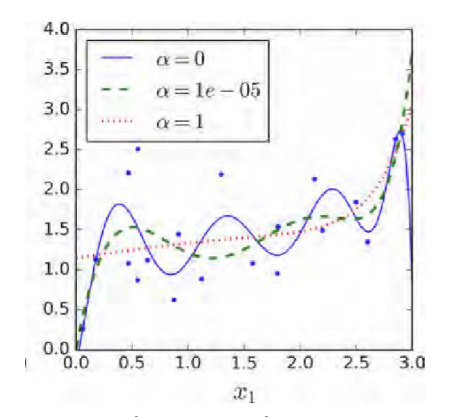
多项式拟合.png

Figure 1 多项式拟合加L2正则化

最小化损失函数时，正则项的存在要求参数 ​\theta 的L2范数越低越好，从而会限制其复杂度。因为L2范数的计算方式是向量所有元素的平方和相加，可以用于形容参数向量整体大小或复杂度，L2范数越大，某些参数的ABS越大，会导致模型过于依赖这些参数。核心逻辑就是压缩无用参数，降低模型复杂度。

可以看出 ​\alpha 越大，拟合的曲线越平滑，因为 ​\alpha 对高维惩罚更严重；反之 ​\alpha 越小，曲线会更弯曲。

L1 LASSO Regression (Least Absolute Shrinkage and Selection Operator Regression)

正则项为参数的绝对值之和，​cost function 为：

J(\theta) = MSE(\theta) + \alpha\Sigma^n_{i=1}|\theta_i|

通过使用更激进的方法：在最小化损失函数时，L1正则项会让不重要的参数直接变成0（不被压缩），最终仅得到稀疏的参数向量，少量关键特征被保留。

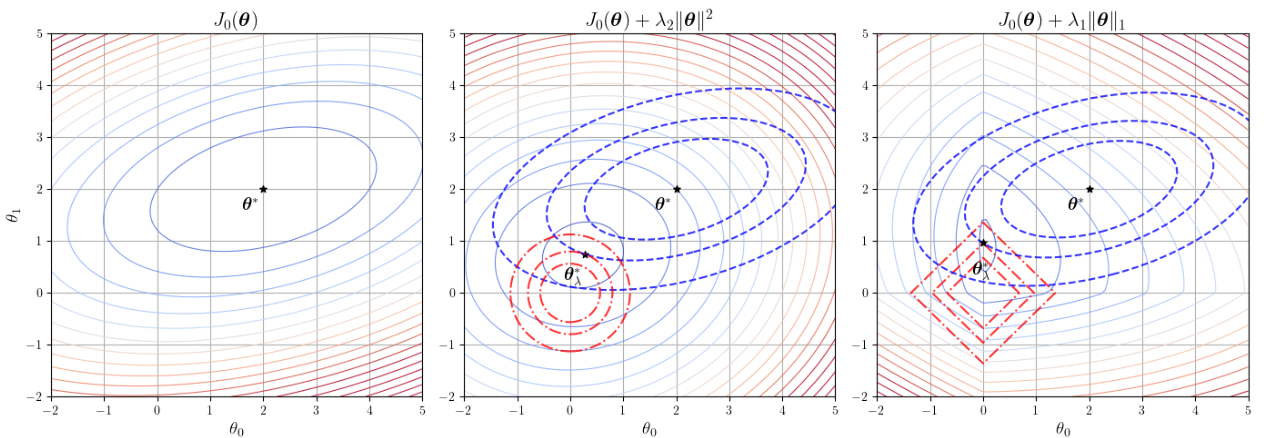
正则化.png

Figure 2 L2&L1正则化约束对比

关于两种正则化形状的解释，注意一个前提，上图是在二维空间。

L1正则化：是权重向量各分量的绝对值之和，在二维情况下，权重向量为​w=(w_1,w_2)，L1正则项是 ​|w_1|+|w_2|=c ，

当 ​w_1 \geq 0, w_2 \geq 0 时，方程为 ​w_1 + w_2 = c

当 ​w_1 \geq 0, w_2 \leq 0 时，方程为 ​w_1 - w_2 = c

当 ​w_1 \leq 0, w_2 \geq 0 时，方程为 ​- w_1 + w_2 = c

当 ​w_1 \leq 0, w_2 \leq 0 时，方程为 ​- w_1 - w_2 = c

这四条直线构成了一个菱形，4个顶点分别为 ​(c,0), (0,c), (-c,0), (0,-c)。损失函数的等高线（通常为椭圆形）与L1正则化约束区域（菱形）的交点更容易出现在顶点上，对应权重向量中有0出现的情况。

L2正则化：是参数平方和的平方根，在二维情况下，表示为 ​\sqrt{w_1^2 + w_2^2} = c，平方后（等价的），在二维平面上就是是圆的标准方程。损失函数的等高线与圆的交点更可能出现在圆周上，而不是在坐标轴上，因此不太可能出现权重向量中有0的情况。

至于为什么要找交点，回顾一下我们的优化目标，是最小化损失函数+正则项这个函数，可以理解为在满足正则化约束（正则项看成一个给定容量的可行域）条件下，找到使损失函数最小的参数向量 ​w。损失函数等高线表示损失函数值相同的 ​w，正则化区域边界表示 ​||w||_p=c 点的集合。

协助理解L1和L2正则化的模式：

理解为行李装箱：

L1正则化：强制丢弃不重要的物品，只保留最关键的物品

L2正则化：压缩所有物品的尺寸，但不会丢弃物品

L1+L2 Elastic Net Regression

J(\theta) = MSE(\theta)+r\alpha\Sigma^n_{n=1}|\theta_i|+\frac{1-r}{2}\alpha\Sigma^n_{i=1}(\theta_i)^2

这种方法，介于L1和L2之间。​\alpha 控制着模型正则化的程度（模型的cost）。若​\alpha非常大，由于结果是一条直线，那么所有参数（​\theta_i）都会是0

模型的选择

  • Ridge 一般作为默认选项
  • 若特征较多，但是有用的较少，可以选择LASSO或者Elastic
  • Elastic比LASSO更优，因为加入了更多的控制项
  • 若特征数量 ​> 训练实例数，选择Elastic

欠拟合与过拟合

训练损失和测试损失都较大，为欠拟合（underfitting）。

训练损失小而测试损失较大，为过拟合（overfitting）。

欠拟合

模型无法拟合数据中的重要模式，模式就是数据背后的规律。

欠拟合会导致预测精度低。

造成欠拟合的因素包括：

  • 模型复杂度太低，不具备学习复杂模式的能力
  • 迭代次数太少，没来得及学习数据的模式
  • 学习率太低，参数更新太慢或不充分

解决欠拟合的方法：

  • 提高模型复杂度，能够学习更复杂的模式
  • 增加迭代次数，欠拟合的训练和测试损失均未收敛，说明模型尚未完全学习数据中的重要模式，增加训练次数可以让模型充分拟合
  • 提高学习率，理由同上

过拟合

过度拟合了训练集数据中，不具备普遍性的部分，在未观测到的数据中，预测效果会变差。

造成过拟合的因素包括：

  • 模型复杂度太高，导致训练损失小，但是预测损失大
  • 训练集的数据太少
  • 训练集噪声太多

解决过拟合的方法：

  • 筛选特征，如PCA
  • 正则化约束
  • Dropout Layer
  • 数据增强，以及增加数据量
  • Early Stop
  • Ensemble Learning
  • 交叉验证

交叉验证 Cross Validation

在训练过程中，一般划分为Training Set和Test Set，但是Test Set对于训练过程来说是未知的，因此常常采取人为构造Test Set的方法，划分出一部分Validation Set。Validation用于模型选择和调参，不用于最终评估。

Validation Set不参与任何模型参数的更新，也就是说模型在训练过程中不应该用到任何Validation Set中的数据信息，如果Test Set和Validation Set的数据分布相同，那么可以认为二者是等效的。

与Test Set的区别见下表：

特性 验证集 测试集
作用 模型选择和调参 最终模型评估
使用频率 多次使用 仅使用一次
数据参与 不参与参数更新 完全不参与训练
评估目的 选择最佳模型 评估模型在真实场景的表现

要注意的是，虽然训练时不会用到Validation Set中的信息，但是如果预处理时用到了Training Set和Validation Set的共同统计信息，那么Validation Set的信息就可以泄露到模型，模型就学到了Training Set以外的信息，因此如果要对数据进行预处理，最好是先划分Set。

在划分不同Set时，常采用随机划分的方式，常用的是交叉验证。

K折交叉验证 K-Fold Cross Validation

将数据集随机划分为K个大小相等的子集，称为Fold，每次使用K-1个子集作为Training Set，剩余的1个子集作为Validation Set。重复K次，每次使用不同的子集作为Validation Set，最终取K次验证结果的平均值作为模型性能的估计。

数据集 → [1][2][3][4][5]（K=5）
第1轮：训练集[2][3][4][5]，验证集[1]
第2轮：训练集[1][3][4][5]，验证集[2]
第3轮：训练集[1][2][4][5]，验证集[3]
第4轮：训练集[1][2][3][5]，验证集[4]
第5轮：训练集[1][2][3][4]，验证集[5]

留一验证 Leave One Out Cross Validation

K-Fold的极端情况，其中K等于数据集大小。每次只留一个样本作为Validation Set，其余所有样本作为Training Set。也就是说需要训练 ​n 次模型，​n 为样本数。

分层K折交叉验证 Stratified K-Fold Cross Validation

在K折交叉验证的基础上，保证每个Fold中各类别样本的比例与原始数据集中的比例一致。特别适用于类别不平衡的数据集。

原始数据集：正类60%，负类40%
K=5的分层K折：
折1：正类60%，负类40%
折2：正类60%，负类40%
...
折5：正类60%，负类40%
© 本文著作权归作者所有，未经许可不得转载使用。