什么是决策树（Decision Trees）

对于决策树，目标变量是连续数值的，被称为回归树；若是离散值，被称为分类树。

比如，预测预测房价，是回归树；预测病患是否患病，是分类树。本文重点介绍分类树。

决策树是一种非参数化模型。

决策树的构造

· 根结点（Root node）：代表整个数据集或采样，并且可以被分为2个或多个同质的集合。
· 决策节点（Decision node）：通过条件判断，决定如何分支。
· 分支/边缘（Branches/Edge）：描述的是选项。
· 叶节点（Leaf）：不包含判断条件，是树的终点，不再分支，包含预测结果。

Figure 1 Decision Tree

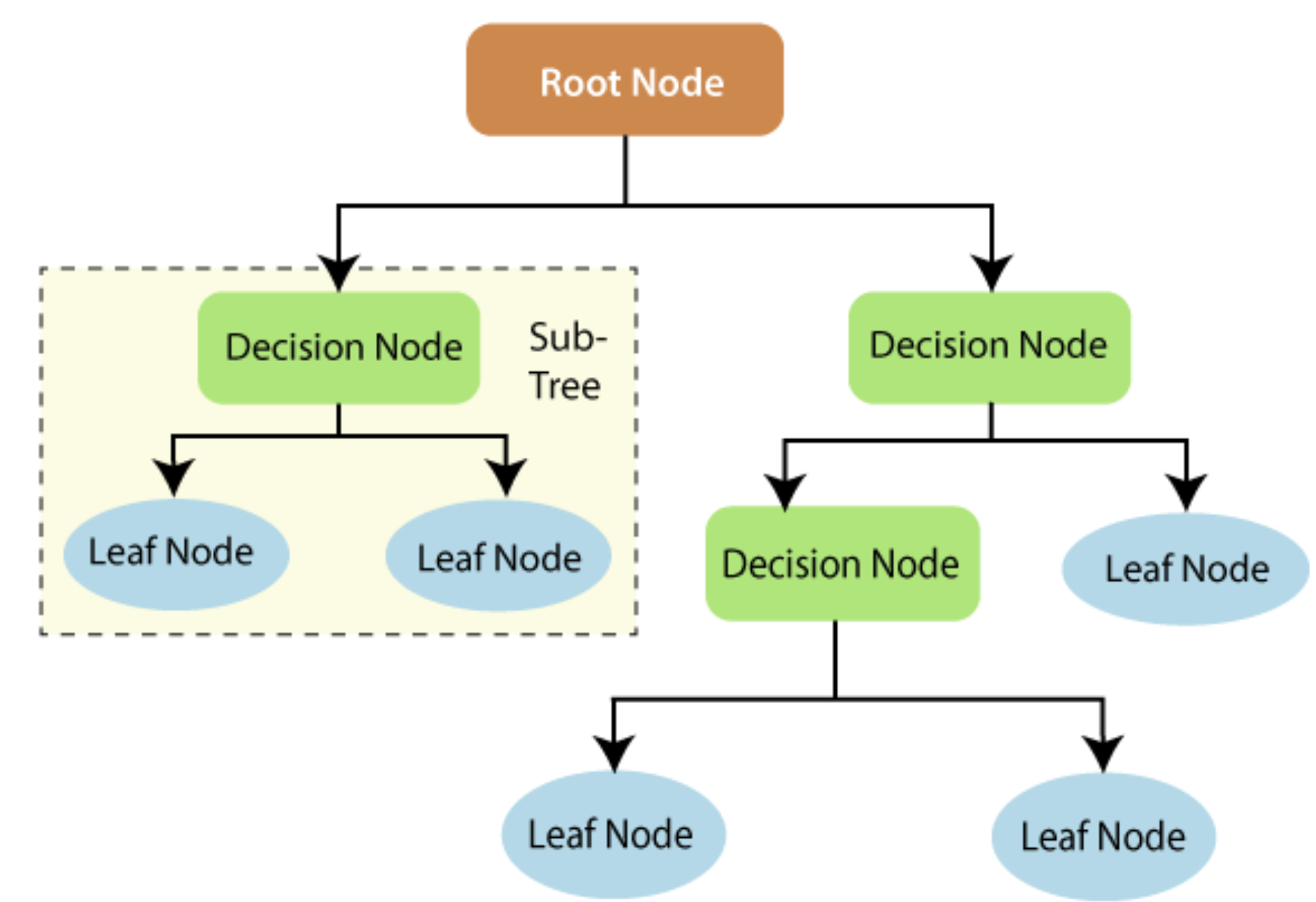
分支策略依赖于数据集的特征，比如颜色，尺寸，形状，等等。

在构造决策树时，我们希望决策树复杂度越低越好。为了实现这一点，每次分类时要尽可能把不同的样本尽可能分开。

决策树的分支

在决策树中，分支准测包括：

Gini impurity 基尼不纯度
Information Gain 信息增益
Chi - Square 卡方检验
Variance Reduction 方差缩减

本文着重介绍信息增益。

熵 Entropy

在信息论中，信息熵的意义就是：一个变量 x 可能的变化越多，那么它携带的信息量越大。对于一个随机事件来说，事件发生的概率越小，那么其提供的信息量越大。

如果一个事件 X_i 发生概率为 P(X_i)，那么所能提供的信息 I 是：

I(X_i)=-\log P(X_i)

可以看出，一个确定事件 P(X_i)=1 不会带来任何信息。

和描述事件的不确定性相似，为了描述系统的不确定程度，引入了熵的概念：

H(X) = -\sum_{i=1}^{n} P(X_i) \cdot \log P(X_i)

熵的公式可以得出一个结论：某个事件发生概率为1，其他事件概率为0，那么H=0；如果每个事件发生概率相等，即P(X_i)=1/n，那么熵最大 H=\log n。

举个例子，一次考试有一道单选题和一道多选题，都是4个选项，全靠蒙。

单选题，正确的概率是1/4，那么这道题答案的熵就是 -4*0.25\log0.25 = 2

多选题，共15种可能，那么这道题答案的熵就是 -15*\cfrac{1}{15}\log\frac{1}{15} = 3.91

系统越是有序，信息熵越低；系统越是混乱，信息熵越大。因此经常使用信息熵作为系统有序化程度的度量。

KL散度

又叫相对熵，可以用于衡量随机变量 X 的两个概率分布 P(x) 和 Q(x) 的距离。

D_{KL}(P \parallel Q) = \sum_{i=1}^{n} P(X_i) \cdot \log \frac{P(X_i)}{Q(X_i)}

在机器学习中，KL散度可以精确衡量用一个近似概率分布 Q 来建模一个真实概率分布 P 时引入的信息损失。

公式可以理解为：在用建模得到的模型 Q 的视角去解释一个事件 X 的时候，所付出的代价。

公式中的 \log \frac{P(x_i)}{Q(x_i)} ，乍一看很抽象，提醒一下，\log 的除法可以写成减法。这里就清楚多了，可以将 P(x_i) 理解为一个权重，乘分布 P 和分布 Q 的距离。加上 \sum 做和，即可得到总代价。

KL散度越大，表示两个分布之间的差异越大；当两个分布完全相同的时候，KL散度为0。

交叉熵

对于离散的随机变量，KL散度可以写为：

\begin{align*} D_{KL}(P \parallel Q) &= \sum_{i=1}^{n} (P(X_i) \cdot \log {P(X_i) - P(X_i) \cdot \log {Q(X_i)})} \\ &= -H(P) - \sum_{i=1}^{n}P(X_i) \cdot \log {Q(X_i)} \\ &= -H(P) + H(P,Q) \end{align*}

其中 H(P,Q) 为分布 P 和 Q 的交叉熵：

H(P, Q) = -\sum_{i=1}^{n} P(X_i) \cdot \log Q(X_i)

在信息论中，交叉熵用于估算平均编码长度，在机器学习中，可以看作概率分布 Q 来表示概率分布 P 的苦难程度。

信息增益

一个数据集，总体的信息量是一定的。

信息增益可以理解为：用某个特征划分数据后（知道某件事后），数据的混乱度降低了多少。混乱度降低的越多，那么这个特征就有更多的信息增益。

条件熵

在给定随机变量X下，随机变量Y的不确定性。定义为在给定X=x_i的条件下，Y的条件概率分布熵对X的数学期望：

\begin{align*} H(Y|X)&=\sum_{i=1}^{n} p(X=x_i) H(Y|X=x_i) \\ &-\sum_{i=1}^{n} P(Y|X=x_i) \log P(Y|X=x_i) \end{align*}

信息增益可以被形容为熵减去条件熵：

g(X,Y) = H(Y)- H(Y|X)

分支的确定

那么如何根据这些准则确定分支？在每个节点处，应有：

最高信息增益
最低熵
最少子节点

但是要注意，在训练的过程中，很有可能出现overfitting的情况，即在每个叶节点，只有一个object
为了避免这种情况，有两种办法，一种是修剪：通过删除使用低重要性特征的分支。

一是对树的尺寸设限制：限制最大树深度，限制最大叶节点数量，限制分支时的最大特征种类，限制分支时最小采样数，限制叶节点最小采样。

分类评价指标

Confusion Matrix (混淆矩阵)

是一种描述分类（Classifier）性能的矩阵。

Figure 2 Confusion Matrix

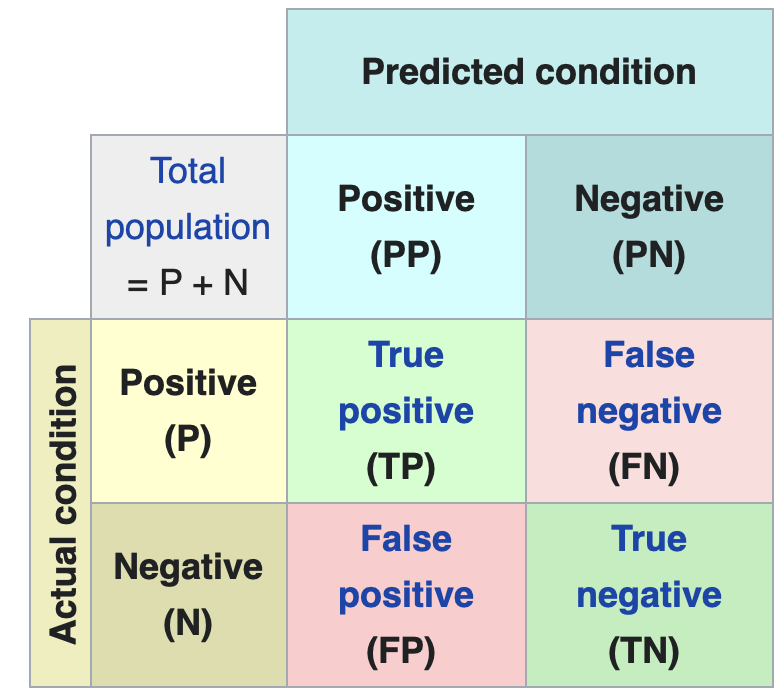
以新冠病毒检测结果为例，

TP：阳性的人，被检测出了阳性，也就是我们的检测目标。
FP：健康的人，被检测出了阳性。假阳性，比如我。
TN：健康的人，被检测为阴性。
FN：阳性的人，被检测为阴性。假阴性，是漏网之鱼。

根据上面4项，可以计算精度（Accuracy），查全率/召回率（Recall），查准率（Precision）这些指标：

Accuracy = \frac{TP+TN}{TP+FN+FP+TN}

Recall = \frac{TP}{TP+FN}

Precision = \frac{TP}{TP+FP}

Fall-out = \frac{FP}{FP+TN}

如果 FN 太多，我们就说这种方法的 recall 很低，自然风险控制能力就很差（放走了携带病毒的人）

如果 FP 太多，我们就说这种方法的 precision 很低，自然这个方法就很浪费（把大量健康人当做携带者处理，成本激增）。

由于样本总数固定，混淆矩阵的 4 个指标并非完全相互独立，因此常用查全率（recall）和查准率（precision）这两个标准作为代表，其他指标的变化也可以通过它们来间接反映。

可以看出，混淆矩阵得出的统计指标不可得兼，为了平衡各个指标，就要用到 F1 分数：

F_1 = \frac{2*recall*precision}{recall+precision}

如果对查全率或查准率的重要程度有所区分，可以设定权重\beta，F1 分数就变成了 F-beta 分数：

F_{\beta} = (1+\beta^2) \frac{recall*precision}{\beta^2 *recall+precision}

比如当 \beta =0.5，那么就是 F_{0.5}。也可以看出，上式 \beta = 0 时，退化为查准率；当 \beta \rarr \inf 时，退化为查全率。

Area Under Curve (AUC) & Receiver Operating Characteristics (ROC)

通过分析不同的指标随着阈值的变化得出的与阈值无关的模型本身特性，以衡量模型在不同阈值下的整体表现。定义假阳性率（FPR）和真阳性率（TPR，即 recall）这两个指标，其中FPR定义为：

FPR= \cfrac{FP}{FP+TN}

当阈值设为0，所有样本都为Positive，无FN和TN，FPR和TPR均为1；随着阈值增大更多样本归为Negative，因此TP和FP减小，TN和FN增大，FPR和TPR减小；当阈值为1之，所有样本都为Negative，FPR和TPR均为0。

因此这两个指标随阈值的变化，产生的变化趋势相同，都随阈值的增大而减小。

把两者的值绘制为ROC曲线。曲线从右上角到左下角，阈值从0增大到1。

如果ROC曲线尽可能的偏向上方，在最好的情况下，会经过左上角，也就是FPR=0，TPR=1的点。不过这只是最理想的情况。

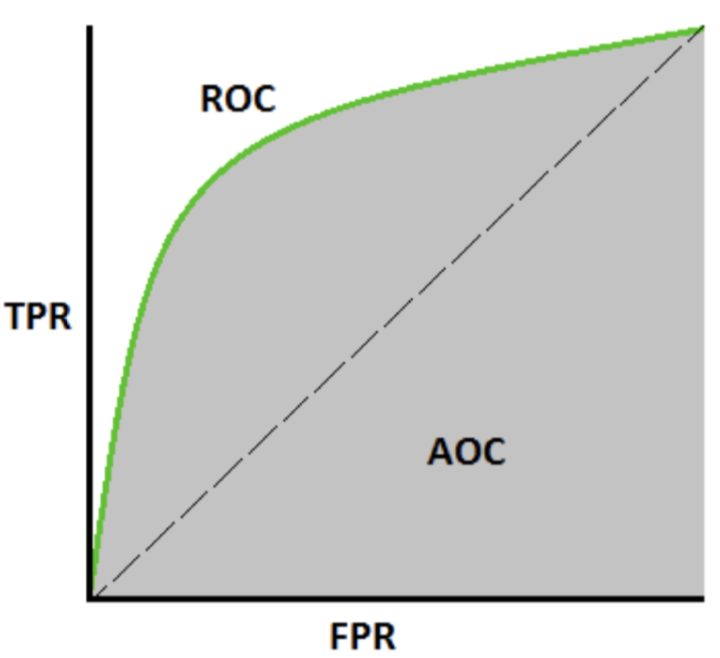
ROC&AUC.png

Figure 3 ROC & AUC

为了定量的衡量ROC曲线反应出的模型性能，计算ROC曲线投影的面积AUC，表示模型分辨两个类别的能力。（为什么PPT写成了AOC。。。好怪）
AUC越大，代表模型越好。AUC一般不会小于0.5（不会纯靠蒙差）。

评价指标总结

这些分类指标大多针对二分类问题，对于多分类，最直观的是准确率（Accuracy）。

而召回率，精确率和 F1 分数，都是针对某个分类计算出的。多分类任务可以针对关注类别计算这几个指标。

站内导航

机器学习 - 决策树 (Decision Tree)